


Next: Monte Carlo K Calculation
Up: MONTE CARLO EIGENVALUE CALCULATION
Previous: Introduction
The time-independent Boltzmann transport equation for neutrons is an equation
for the neutron angular density. This equation is derived by applying neutron
conservation to an infinitesimal element of volume, direction and energy
[Bell70, Lew93]. The integro-differential form of the time-independent
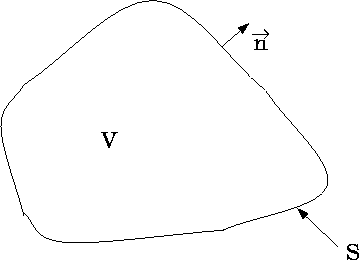
transport equation in a medium with volume V surrounded by a surface S,
as shown in figure 2.1, can be written as,
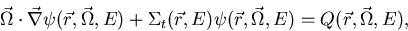
| 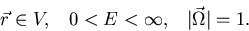 |
(1) |
Figure:
Spatial Domain V for the Transport Equation with Surface S.
 |
The boundary condition, if 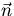 is an outward normal to S, is given as,
is an outward normal to S, is given as,
| 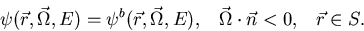 |
(2) |
In the transport equation, 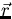 denotes spatial variables, E denotes
energy,
denotes spatial variables, E denotes
energy, 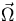 denotes angular variables,
denotes angular variables, 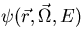 is the angular flux,
is the angular flux, 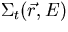 is the macroscopic total cross
section, and
is the macroscopic total cross
section, and 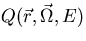 is the source emission density.
is the source emission density.
In general, the source emission density 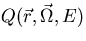 consists of
three contributors:
consists of
three contributors:
The above three contributors are due to the external source, scattered
particles, and fission neutrons, respectively.
For nonmultiplying systems Qf=0, and the two contributions to the source
emission density are due to the external source and the scattered particles.
Hence the transport equation in a nonmultiplying medium is given by,
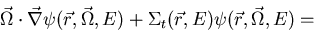
| 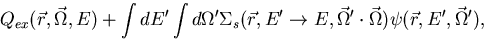 |
(4) |
where 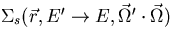 is the macroscopic scattering cross section.
is the macroscopic scattering cross section.
For multiplying media, the contribution Qf due to the neutrons emitted from
fission reactions must be included. We will assume that all neutrons are
produced instantaneously at the time of fission and neglect the effect of
delayed neutrons. This is a valid assumption, except for time dependent
problems of neutron kinetics. This assumption is appropriate for steady state
problems with fixed sources and for criticality calculations, where only the
critical state and the flux distribution are of interest. The transport
equation in a multiplying medium without delayed neutrons takes the following
form:
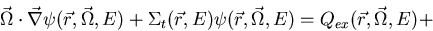
| 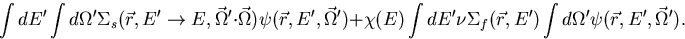 |
(5) |
Here, 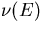 is the mean number of fission neutrons produced in a fission caused
by a neutron with energy E. The effect of delayed neutrons is included in
the total
is the mean number of fission neutrons produced in a fission caused
by a neutron with energy E. The effect of delayed neutrons is included in
the total 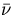 . Also
. Also 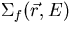 is the macroscopic fission
cross section and
is the macroscopic fission
cross section and 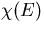 denotes the fission spectrum. The transport
equation is a hyperbolic equation in both the time dependent and steady state
forms. In a nonmultiplying medium with a steady state source, there exists a
steady state flux distribution that satisfies this equation [Cas67]. In
multiplying
systems, the transport equation is studied by introducing the concept of criticality.
Physically,
a system containing fissionable material is critical if a self-sustaining
time independent chain reaction in the absence of external neutron sources can
be maintained. Mathematically, a system is critical if it has a
time-independent, nonnegative solution to the transport equation without
external
source, i.e.
denotes the fission spectrum. The transport
equation is a hyperbolic equation in both the time dependent and steady state
forms. In a nonmultiplying medium with a steady state source, there exists a
steady state flux distribution that satisfies this equation [Cas67]. In
multiplying
systems, the transport equation is studied by introducing the concept of criticality.
Physically,
a system containing fissionable material is critical if a self-sustaining
time independent chain reaction in the absence of external neutron sources can
be maintained. Mathematically, a system is critical if it has a
time-independent, nonnegative solution to the transport equation without
external
source, i.e.
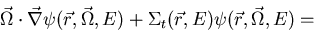
| 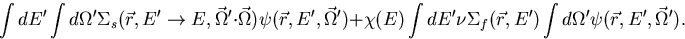 |
(6) |
In general, it is difficult to find that combination of cross sections and
geometry that will allow equation (2.6) to be satisfied.
Therefore, for criticality calculations, the above equation is cast into the
form of an
eigenvalue problem. The eigenvalue provides a measure of the criticality of
the system. Two formulations for criticality are the time-absorption or
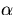 -eigenvalue formulation and the multiplication factor
formulation
with the K eigenvalue [Bell70]. The K eigenvalue approach is discussed
in this thesis.
-eigenvalue formulation and the multiplication factor
formulation
with the K eigenvalue [Bell70]. The K eigenvalue approach is discussed
in this thesis.
We have stated before that K can be defined as the quantity by which 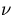 must be divided to keep a system critical, i.e.,
must be divided to keep a system critical, i.e., 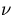 can be adjusted to obtain
a time independent solution to equation (2.6). Hence for the K eigenvalue problem
can be adjusted to obtain
a time independent solution to equation (2.6). Hence for the K eigenvalue problem
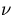 is replaced by
is replaced by 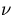 /K and the transport equation becomes,
/K and the transport equation becomes,
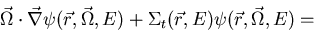
| 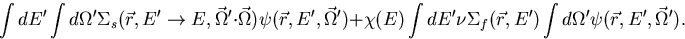 |
(7) |
In an eigenvalue problem it is always possible to find the largest
value of K that will give a nonnegative fundamental mode solution to equation
2.7. The
system is critical
if this largest value of K is equal to unity. If K < 1, then 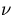 , the
actual number of neutrons per fission available, is less than
, the
actual number of neutrons per fission available, is less than 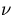 /K,
the number of neutrons per fission necessary to maintain criticality, and
the system is subcritical. Similarly
/K,
the number of neutrons per fission necessary to maintain criticality, and
the system is subcritical. Similarly
for
K > 1, the actual number of
neutrons per fission, 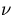 , is more than
, is more than 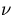 /K, the number of neutrons per
fission required to
maintain the system critical, and hence the system is supercritical.
/K, the number of neutrons per
fission required to
maintain the system critical, and hence the system is supercritical.
Equation (2.7) is the integro-differential form of the transport equation.
This equation can also be expressed in integral form using the Green's
function. The Green's function G(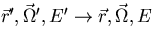 ) is the neutron angular flux at
) is the neutron angular flux at 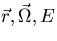 due to
a unit point source at
due to
a unit point source at 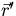 emitting 1 neutron/sec in the direction
emitting 1 neutron/sec in the direction
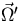 with energy E'. Using the Green's function we
can write down the K
eigenvalue equation as follows:
with energy E'. Using the Green's function we
can write down the K
eigenvalue equation as follows:
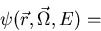
| 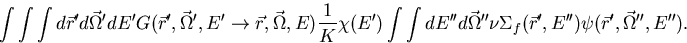 |
(8) |
Both equation (2.7) and (2.8) can be expressed in terms of the fission source
density, 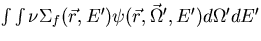 , which gives the spatial distribution of fission neutrons. From
that form, both equations lead to the same matrix eigenvalue problem, to
which the power iteration method can be applied to calculate K, as
explained below.
, which gives the spatial distribution of fission neutrons. From
that form, both equations lead to the same matrix eigenvalue problem, to
which the power iteration method can be applied to calculate K, as
explained below.
For the time-independent, nonmultiplying transport equation given in equation
(2.4), the transport operator is defined as [Lew93]:
![\begin{displaymath}
H\psi = [\vec \Omega \cdot \vec \nabla + \Sigma
_t(\vec r,E)] \psi (\vec r,\vec \Omega,E ) \end{displaymath}](img30.gif)
| 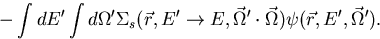 |
(9) |
Expressing the fission source density as,
| 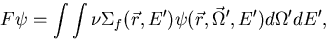 |
(10) |
the multiplication eigenvalue problem, equation (2.7), can be written in
operator notation as
| 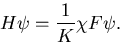 |
(11) |
Inverting H and operating on both sides by F, we obtain the following
form of the eigenvalue problem:
| ![\begin{displaymath}
F \psi = \frac {1}{K}[F H^{-1} \chi] F \psi .\end{displaymath}](img34.gif) |
(12) |
Using the following definition for the transport operator
| 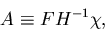 |
(13) |
the eigenvalue equation becomes,
where S ( = F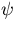 ) is the source eigenvector and A is the fission matrix.
The element A(l,m) of the fission matrix represents the probability that a
neutron starting in cell m will generate a fission neutron appearing in cell l.
In integral form, the above equation can be expressed as,
) is the source eigenvector and A is the fission matrix.
The element A(l,m) of the fission matrix represents the probability that a
neutron starting in cell m will generate a fission neutron appearing in cell l.
In integral form, the above equation can be expressed as,
| 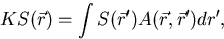 |
(15) |
where A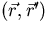 is the operator that describes the probability
that a neutron originating at
is the operator that describes the probability
that a neutron originating at 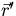 produces a fission neutron at
produces a fission neutron at
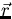 and S
and S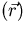 is the source distribution.
The above equation can also be derived from the integral transport form of the
K eigenvalue equation ( equation (2.8) ) by using the operator F and
the following property of the Green's function:
is the source distribution.
The above equation can also be derived from the integral transport form of the
K eigenvalue equation ( equation (2.8) ) by using the operator F and
the following property of the Green's function:
| 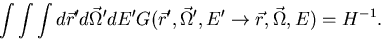 |
(16) |
The multiplication eigenvalue problem of equation (2.14) is then
solved by the method of power iteration [Var62, Wac66, Nak77].



Next: Monte Carlo K Calculation
Up: MONTE CARLO EIGENVALUE CALCULATION
Previous: Introduction
Amitava Majumdar
9/20/1999
![]()
![]() is an outward normal to S, is given as,
is an outward normal to S, is given as,
![]() consists of
three contributors:
consists of
three contributors:
![]()
![]()
![]()
![]() must be divided to keep a system critical, i.e.,
must be divided to keep a system critical, i.e., ![]() can be adjusted to obtain
a time independent solution to equation (2.6). Hence for the K eigenvalue problem
can be adjusted to obtain
a time independent solution to equation (2.6). Hence for the K eigenvalue problem
![]() is replaced by
is replaced by ![]() /K and the transport equation becomes,
/K and the transport equation becomes,
![]()
![]() ) is the neutron angular flux at
) is the neutron angular flux at ![]() due to
a unit point source at
due to
a unit point source at ![]() emitting 1 neutron/sec in the direction
emitting 1 neutron/sec in the direction
![]() with energy E'. Using the Green's function we
can write down the K
eigenvalue equation as follows:
with energy E'. Using the Green's function we
can write down the K
eigenvalue equation as follows:
![]()
![]()