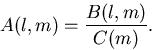
We have mentioned in section 2.3.2. that there are two variations of the fission matrix algorithm. In this section we introduce these two variations and perform numerical experiments to study the effect of these two algorithms on different test problems. In section 2.3.2 the fission matrix algorithm was described. We have shown that for every collision that occurs in a cell l, we accumulate in a matrix B(l,m) the contribution to K due to a neutron that started from cell m. An array C(m) stores the number of neutrons that started from cell m. After all histories are tracked, the fission matrix A(l,m) is computed as
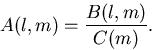 |
(32) |
The first variation of the fission matrix algorithm, called the cycle fission matrix (cyfm) algorithm, zeroes out all elements of the matrix B(l,m) and the array C(m) at the begining of each batch. Hence, the fission matrix is formed only from the contribution of all neutrons of a particular batch. The batch K is calculated at the end of each batch, along with the batch averaged K over all batches, and the standard deviation of the batch averaged K. Fission source normalization is done using the batch K. Since the fission matrix is computed for every batch, independent of any contribution from previous batches, the batch Ks are independent and we can calculate the batch averaged K and the associated standard deviation.
The second variation, called the cumulative fission matrix (cumfm) algorithm, does not zero out elements of the matrix B(l,m) and the array C(m) at the begining of each batch. Contributions to both B(l,m) and C(m) are accumulated over batches and the fission matrix A(l,m) is computed from them. At the end of each batch we calculate the batch K. Since contributions to the fission matrix are accumulated over batches, the batch eigenvalues are not independent in a statistical sense, and hence the batch averaged eigenvalue and the associated standard deviation are not computed. The batch K is used for fission source normalization.
We now perform computational experiments to see the effect of these two fission matrix algorithms on different test problems. We will specifically look at the effect of these algorithms on loosely coupled versus tightly coupled problems. Effects of different batch sizes, inactive and active batches will also be studied. The test cases [Urb95b] are slab geometry problems, with isotropic scattering and vacuum boundaries.
The first test problem is a tightly coupled problem consisting of a
60 mfp homogeneous slab with ![]() = 1.0,
= 1.0,
![]() = 0.7,
and
= 0.7,
and ![]() = 0.3071. A fine mesh S32 calculation gives a K of
1.02070
for this test problem. Results for this test problem are shown in table 2.4 for
different batch sizes and for different numbers of inactive and active batches.
We observe from table 2.4 that both fission
matrix algorithms perform equally well. We cannot differentiate one being
superior to the other algorithm for this test problem. For this test problem
the effect of different batch sizes and different
numbers of inactive and active batches is not significant.
= 0.3071. A fine mesh S32 calculation gives a K of
1.02070
for this test problem. Results for this test problem are shown in table 2.4 for
different batch sizes and for different numbers of inactive and active batches.
We observe from table 2.4 that both fission
matrix algorithms perform equally well. We cannot differentiate one being
superior to the other algorithm for this test problem. For this test problem
the effect of different batch sizes and different
numbers of inactive and active batches is not significant.
The second test problem, which is a loosely coupled problem,
is a lattice of fuel regions and absorber regions. The
fuel regions are each 2 cm thick and are separated by 1 cm thick regions of
absorbing material. The material at the boundaries is another 1 cm slab of
absorbing material. There are 19 fuel regions and the thickness of the entire
slab is 58 cm. Cross sections of the fuel regions are ![]() =1.0,
=1.0,
![]() =0.7, and
=0.7, and ![]() =0.3071; and cross sections of the absorbing
regions are
=0.3071; and cross sections of the absorbing
regions are ![]() =1.0,
=1.0, ![]() =0.001, and
=0.001, and ![]() =0.0.
A fine mesh TWODANT calculation gives a K of 0.59852 for this problem.
Results for this test problem are shown in table 2.5 for
different batch sizes and for different numbers of inactive and active batches.
We observe from table 2.5 that the cumulative fission matrix algorithm
performs better than the cycle fission matrix algorithm. The test problem is a
loosely coupled problem due to the strong absorbing materials separating
fuel
regions. Sampling only with neutrons of each batch does not provide good
enough sampling for fission reaction, and hence the cycle fission matrices do
not represent the loosely coupled system well. Even for the last case of table
2.5, i.e., with 5000 neutrons per batch, the eigenvalue has not reached the
=0.0.
A fine mesh TWODANT calculation gives a K of 0.59852 for this problem.
Results for this test problem are shown in table 2.5 for
different batch sizes and for different numbers of inactive and active batches.
We observe from table 2.5 that the cumulative fission matrix algorithm
performs better than the cycle fission matrix algorithm. The test problem is a
loosely coupled problem due to the strong absorbing materials separating
fuel
regions. Sampling only with neutrons of each batch does not provide good
enough sampling for fission reaction, and hence the cycle fission matrices do
not represent the loosely coupled system well. Even for the last case of table
2.5, i.e., with 5000 neutrons per batch, the eigenvalue has not reached the
| 1|cFine mesh | 1cTWODANT | 1c K = | 1c|1.02070 |
| 1|c#of neutrons/batch | 1|c|Ii, Ia | 1|c|cyfm | 1c|cumfm |
| 500 | Ii=0,Ia=80 | 1.02053 |
1.01923 |
| 500 | Ii=20,Ia=60 | 1.02096 |
1.01923 |
| 1000 | Ii=0,Ia=80 | 1.02072 |
1.01995 |
| 1000 | Ii=20,Ia=60 | 1.02123 |
1.01995 |
| 1500 | Ii=0,Ia=80 | 1.02026 |
1.01991 |
| 1500 | Ii=20,Ia=60 | 1.02079 |
1.01991 |
| 2000 | Ii=0,Ia=80 | 1.01989 |
1.01946 |
| 2000 | Ii=20,Ia=60 | 1.02019 |
1.01946 |
| 3000 | Ii=10,Ia=150 | 1.020080 |
1.02011 |
| 3000 | Ii=50,Ia=150 | 1.02024 |
1.02011 |
| 4000 | Ii=10,Ia=150, | 1.020324 |
1.01993 |
| 4000 | Ii=50,Ia=150, | 1.020564 |
1.01993 |
| 5000 | Ii=10,Ia=150, | 1.020732 |
1.02023 |
| 5000 | Ii=50,Ia=150, | 1.021019 |
1.02023 |
| 1|cFine mesh | 1cTWODANT | 1c K = | 1c|0.59852 |
| 1|c# of neutrons/batch | 1|c|Ii, Ia | 1|c|cyfm | 1c|cumfm |
| 500 | Ii=0,Ia=80 | 0.791 |
0.6005 |
| 500 | Ii=20,Ia=60 | 0.792 |
0.6005 |
| 1000 | Ii=0,Ia=80 | 0.6971 |
0.59925 |
| 1000 | Ii=20,Ia=60 | 0.7024 |
0.59925 |
| 1500 | Ii=0,Ia=80 | 0.6504 |
0.59872 |
| 1500 | Ii=20,Ia=60 | 0.6512 |
0.59872 |
| 2000 | Ii=0,Ia=80 | 0.6466 |
0.59953 |
| 2000 | Ii=20,Ia=60 | 0.6512 |
0.59953 |
| 3000 | Ii=10,Ia=150 | 0.6268 |
0.60026 |
| 3000 | Ii=50,Ia=150 | 0.6289 |
0.60026 |
| 4000 | Ii=10,Ia=150, | 0.61862 |
0.59909 |
| 4000 | Ii=50,Ia=150, | 0.6189 |
0.59909 |
| 5000 | Ii=10,Ia=150, | 0.6176 |
0.59883 |
| 5000 | Ii=50,Ia=150, | 0.6188 |
0.59883 |
correct fine mesh result for the cycle fission matrix algorithm. We observe that as the number of neutrons per batch is increased, the cycle fission matrix eigenvalue approaches the correct result. This indicates that a large number of neutrons per batch is necessary for the cycle fission matrix algorithm to perform well for this test problem. In figure 2.11 we plot the batch eigenvalue and the batch averaged eigenvalue of the cycle fission matrix algorithm and the batch eigenvalue of the cumulative fission matrix algorithm for the first test problem with 5000 neutrons per batch and Ii=50 and Ia=100. Only the last 40 batches are shown in figure 2.11. From this figure we notice that the batch eigenvalue of the cumulative fission matrix is far superior to the batch eigenvalue of the cycle fission matrix, as expected, whereas the batch averaged eigenvalue of the cycle fission matrix and the batch eigenvalue of the cumulative fission matrix show comparable accuracy. Figure 2.12 shows similar plot for second test problem. From figure 2.12 it is clear that the cumulative fission matrix algorithm yields superior results to the cycle fission matirx algorithm for loosely coupled problems.
Numerical experiments with other test problems have also shown similar behaviour. We can make a few conclusions from these numerical experiments. As expected, the batch eigenvalue of the cumulative fission matrix algorithm always provides superior result compared to the batch eigenvalue of the cycle fission matrix algorithm. The batch eigenvalue of the cumulative fission matrix algorithm and the batch averaged eigenvalue of the cycle fission matrix algorithm provide comparable results for tightly coupled problems, where there is enough neutron communication between different regions. For a loosely coupled system, the cumulative fission matrix eigenvalue result is superior to the batch averaged eigenvalue of the cycle fission matrix algorithm. For this kind of system, the cycle fission matrix algorithm should be used with caution.