


Next: Statistics for Monte Carlo
Up: Monte Carlo K Calculation
Previous: Monte Carlo K Estimators
The source iteration and fission matrix algorithms for Monte
Carlo criticality calculations are discussed
below using the collision estimator. For simplicity of notation, we assume a
homogeneous system made up of a single isotope material that has cross sections
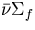 ,
, 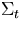 and
and 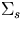 .
.
Source Iteration Algorithm:
The source iteration method is formulated by solving the source equation (equation
(2.15)),
| 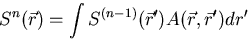 |
(21) |
and calculating K as the ratio of source neutrons of two successive neutron
generations [Uss58, Men68] as follows:
| 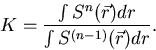 |
(22) |
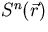 is the source distribution of the nth generation of
neutrons and
is the source distribution of the nth generation of
neutrons and 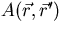 describes the probability that a neutron
originating at
describes the probability that a neutron
originating at 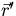 produces a fission neutron at
produces a fission neutron at 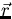 . The Monte
Carlo source iteration algorithm is given below:
. The Monte
Carlo source iteration algorithm is given below:
- 1.
- N source neutrons are started with an initial guessed spatial
distribution. Each neutron has a starting weight W = 1.0.
- 2.
- At every collision point where fission is possible we perform the following
operations.
- (a)
- Accumulate the tally for the collision estimator,
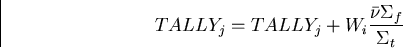
where,
i = each collision by the neutron, and
j = all neutrons, j = 1,2,....,N.
- (b)
- We record the location and the number (n'i) of source
neutrons to
be started from that location (where collision occurred)
for the next generation:
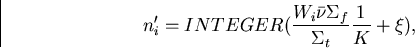
where 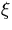 is a random number between 0 and 1, and K is the last batch's
eigenvalue or a guessed one for the first batch.
is a random number between 0 and 1, and K is the last batch's
eigenvalue or a guessed one for the first batch.
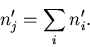
- (c)
- For survival biasing, we set the new weight after the ith
collision, Wi+1, to,

- (d)
- We also apply the Russian roulette technique [Lew93]
to eliminate low weight neutrons.
- 3.
- After all the N neutron histories have been tracked, the eigenvalue for
that generation or batch is calculated as;
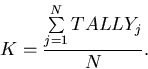
- 4.
- The next batch is started with N' source neutrons, where
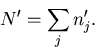
For this next batch each source particle has a starting weight,
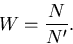
This completes the source iteration algorithm. It should be noted that
the number of neutrons, started in each batch, times the weight of each neutron,
for that batch, is constant for the all batches, i.e.,
W*N' is same for all the batches. N' is close to N due to the K
normalization done in step 2(b). If the initial guess of K is too low or too
high, the number of fission neutrons produced for the next batch will be too high
or too low relative to the desired nominal number N. The number of fission
neutrons, ni' stored at
each collision is rounded up or down (step 2(b)) to an integer (including zero)
with a probability proportional to its deviation from that integer.
Fission Matrix Algorithm:
The fission matrix method [Kap58, Mih67] solves the eigenvalue equation
| 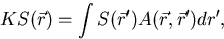 |
(23) |
which holds for every generation. Equation (2.23) can be discretized and is
then reduced to the matrix equation,
where S is the source eigenvector and A is the fission matrix. The element
A(l,m) of the fission matrix describes the probability that a neutron starting
in cell m will generate a fission neutron in cell n [Ave58]. Assuming that the
physical space is discretized into M cells, the Monte Carlo
fission matrix algorithm can be described as:
- 1.
- N source neutrons are started with an initial guessed spatial
distribution. Each neutron has a starting weight W = 1.0. An array C(m) keeps
track of the number of neutrons that start from cell m where m = 1,2,...,M.
- 2.
- At every collision point where fission is possible, the following
operations are performed:
- (a)
- If the collision occurs in cell l, accumulate into matrix B(l,m)
the contribution to K due to a
neutron that started from cell m, i.e.,
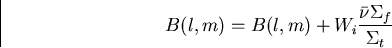
where
i = every collision that a neutron encounters and 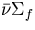 and
and
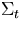 are macroscopic cross sections for cell l.
are macroscopic cross sections for cell l.
- (b)
- Record the location and the number (n'i) of source
neutrons to
be started from that location (where collision occurred) for the
next generation.
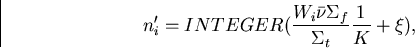
where 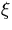 is a random number between 0 and 1, and K is the previous batch
eigenvalue (or a guessed one for the first batch).
is a random number between 0 and 1, and K is the previous batch
eigenvalue (or a guessed one for the first batch).
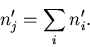
- (c)
- For survival biasing, adjust the new weight after the ith
collision,

- (d)
- Apply the Russian roulette technique [Lew93] to eliminate low weight
neutrons.
- 3.
- After all the N neutron histories have been tracked, compute the
fission matrix A(l,m) element,
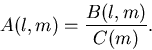
The element A(l,m) gives the expected number of fission neutrons produced in
cell l due to a unit source neutron in cell m. The dominant eigenvalue, or
K, of
the fission matrix A can be calculated by using a matrix iterative algorithm.
- 4.
- Start the next batch with N' source neutrons, where
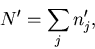
where each source particle has a starting weight,
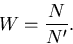
This completes the fission matrix algorithm.
As with source iteration, the quantity W*N' is preserved for all batches.
There are two ways to formulate the fission matrix algorithm. These two
formulations are
explained in detail in section 2.5. The numerical examples of section 2.4 are
solved using the cycle fission matrix approach, where the elements of the matrix
B(l,m) and the array C(m) are zeroed out at the begining of every batch.
The following information is provided to a Monte Carlo eigenvalue simulation
algorithm:
- the nominal number of source histories per batch;
- the initial guess of K;
- the number of initial batches, Ii, to be discarded before tally
accumulation;
- the total number of batches, It, for the problem; and
- an initial spatial distribution for the source.
The number of active batches, Ia that are used to evaluate the mean
and the standard
deviation for K is then given by,



Next: Statistics for Monte Carlo
Up: Monte Carlo K Calculation
Previous: Monte Carlo K Estimators
Amitava Majumdar
9/20/1999
![]() ,
, ![]() and
and ![]() .
.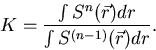
![]()
![]()
![]()
![]()
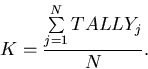
![]()
![]()
![]()
![]()
![]()
![]()
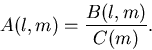
![]()
![]()