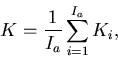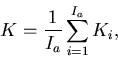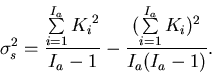Statistics for Monte Carlo K Calculation

A Monte Carlo eigenvalue simulation provides the following estimate of the average eigenvalue,

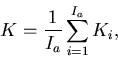$$K = \frac{1}{I_a}\sum\limits_{i=1}^{I_a}{K_i},$$ (26)

where K_i is the batch eigenvalue. The sample variance in this estimate of K is

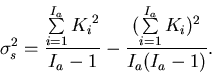$$\sigma_s^2 = \frac{\sum\limits_{i=1}^{I_a}{K_i}^2}{I_a - 1} - \frac {({\sum\limits_{i=1}^{I_a}{K_i}})^2}{I_a(I_a-1)}.$$ (27)

The standard deviation is then

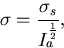$$\sigma = \frac{\sigma_s}{I_a^{\frac{1}{2}}},$$ (28)

which is provided along with the average eigenvalue estimate. The expressions for the variance and standard deviations assume that the batch eigenvalues are independent, hence no batch-to-batch correlations exist after the fundamental eigenmode is reached.