Issues Related to Monte Carlo K Calculation

The first issue that needs to be addressed regarding Monte Carlo K calculations is that of source convergence. Before accumulating any K tally data, enough batches must be performed and discarded to allow the source neutron distribution to attain the fundamental mode [Whi71]. Good spatial sampling is important for attaining and maintaining the fundamental eigenmode. Maintaining the fundamental eigenmode may be difficult, especially for systems with high dominance ratio, due to the batch-to-batch correlations in the spatial distributions of fission neutrons. This is due to the fact that for systems with high dominance ratio, there is less neutron communication between different regions of the system and spatial correlations between batches may prevail.

The second issue deals with the assumption that the batch eigenvalues are independent. For systems with a high dominance ratio, batch-to-batch correlations among fission neutron distribution exist, and this assumption is invalid. This results in an underestimation of the standard deviation [Moo76, Gel90a]. Various studies [Mac73, Gas75] have been done to account for this phenomenon.

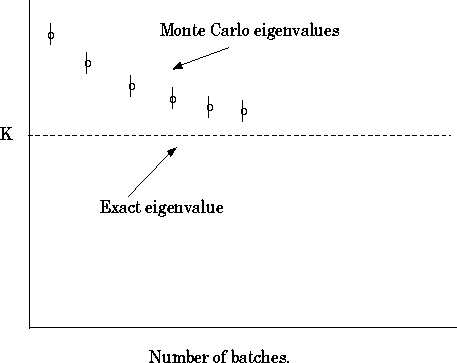
The third issue involves the choice of the optimum number of batches versus the optimum number of neutrons per batch [Lew93], as illustrated in figures 2.2 and 2.3. Figure 2.2 pertains to the case where a large number of neutrons per batch has been followed for a few batches, while figure 2.3 shows the case where a small number

 

Figure: Few Batches with Large Number of Histories per Batch.

of neutrons per batch was followed for a large number of generations. Note that in figure 2.2, the fundamental eigenmode is not reached, even though the variance in the eigenvalue estimate is small. On the other hand, figure 2.3 shows that the fundamental

 

Figure: Large Number of Batches with Few Histories per Batch.

eigenmode is reached, albeit with a large variance in the eigenvalue estimator.

Lastly, we address the issue of bias in Monte Carlo eigenvalue calculation [Gel91]. The bias is a result of the fission source normalization done after each batch. Numerical experiments [Bow83] suggest that biases in fluxes and eigenvalues are negligibly small for most practical cases. The conclusion that, in practice, the eigenvalue bias is negligible and smaller than a single standard deviation, also has strong theoretical support [Gel90b]. A detailed analysis of bias [Bri86, Gel94] gives the following equation;

$$E\{K_0\} = \lambda_0 - (\frac{N_G}{2\lambda_0})({\sigma_t}^2 - {\sigma_a}^2),$$ (29)

where,
K₀ is the biased Monte Carlo eigenvalue computed by averaging over generations or batches;
$\lambda_0$ is the true eigenvalue;
${\sigma_t}^2$ is the true variance in K₀;
${\sigma_a}^2$ is the apparent variance in K₀, computed by assuming that estimates of K from different generations are independent; and
N_G is the active number of generations.
Thus the bias, $\Delta\lambda$, is given by,

$$\Delta\lambda = -\frac{N_G}{2\lambda_0}({\sigma_t}^2 - {\sigma_a}^2),$$ (30)

and the relative bias (compared to the standard deviation) is bounded by

$$\frac{\vert\Delta\lambda\vert}{\sigma_t} < \frac{N_G}{2}\frac{\sigma_t}{\lambda_0}.$$ (31)

For typical eigenvalue calculations one prefers $\frac{\sigma_t}{\lambda_0} < 0.0025$, and hence if N_G is less than 800 the bias will be less that a standard deviation [Gel90a]. It should be noted that the bias itself is independent of N_G since ${\sigma_t}^2$ is proportional to $\frac{1}{N_G}$. Therefore, an adequate number of histories per batch should be tracked; and a number of batches should be simulated which is statistically large enough, but not so large such that the bias in the estimate of K is a significant fraction of the standard deviation.