


Next: Correlated Sampling Technique
Up: Difficulties of Monte Carlo
Previous: Difficulties of Monte Carlo
Numerical examples are provided here to demonstrate
that straightforward subtraction
of two independent Monte Carlo simulations is problematical for calculating
small perturbation effects. All the test problems correspond to
a homogeneous, one
energy group, slab, with thickness of 16 cm and vacuum boundary conditions on
both ends. Table 3.1 shows the unperturbed and perturbed
cross sections and 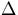 K results calculated by two independent Monte Carlo
simulations and the reference TWODANT simulation. Monte Carlo results are
for 30 inactive
batches, 70 active batches and 2000 neutrons per batch. The
TWODANT results were
generated using S32 quadrature sets and inner and outer iteration
convergence criteria of 10-12.
K results calculated by two independent Monte Carlo
simulations and the reference TWODANT simulation. Monte Carlo results are
for 30 inactive
batches, 70 active batches and 2000 neutrons per batch. The
TWODANT results were
generated using S32 quadrature sets and inner and outer iteration
convergence criteria of 10-12.
Table:
Perturbation Results from Independent Monte Carlo Simulations.
| 1|cUnperturbed |
1ccross sections: |
1c |
1c| |
1|c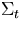 =1.0 cm-1, =1.0 cm-1, |
1c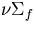 =0.11 cm-1, =0.11 cm-1, |
1c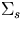 =0.9 cm-1 =0.9 cm-1 |
1c| |
| 1|cProblem # |
1|c|Perturbed cross sections |
1|c|TWODANT 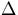 K K |
1c|Monte Carlo 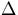 K K |
| 1 |
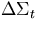 =.001, =.001, 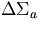 =.001 =.001 |
-.008807 |
-.00843 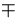 .89E-3 .89E-3 |
| 2 |
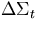 =.0001, =.0001, 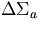 =.0001 =.0001 |
-.000888 |
.00033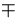 .89E-3 .89E-3 |
| 3 |
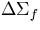 =.0001 =.0001 |
.000903 |
.00124 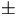 .86E-3 .86E-3 |
Results of table 3.1 show, with the exception of the first test problem,
that subtracting two
independent Monte Carlo runs to calculate small perturbation effects can yield
significant errors. Similar observations can be found in other references
[Wal94, Gal95] also. Later in this chapter (in section 3.3.4), test
problems 1,
2 and 3 are solved
using the combined correlated sampling fission matrix (CSFM) approach
(with the same number of batches and neutrons per
batch as in the cases of table 3.1) and the results are significantly more
accurate than in table 3.1. Also, later in this chapter, it is shown that
when
the correlated sampling technique is applied with
the source iteration method, it encounters severe difficulties; and
it is found that the combined CSFM method yields far
superior results in Monte Carlo calculations of perturbation effects.



Next: Correlated Sampling Technique
Up: Difficulties of Monte Carlo
Previous: Difficulties of Monte Carlo
Amitava Majumdar
9/20/1999
![]() K results calculated by two independent Monte Carlo
simulations and the reference TWODANT simulation. Monte Carlo results are
for 30 inactive
batches, 70 active batches and 2000 neutrons per batch. The
TWODANT results were
generated using S32 quadrature sets and inner and outer iteration
convergence criteria of 10-12.
K results calculated by two independent Monte Carlo
simulations and the reference TWODANT simulation. Monte Carlo results are
for 30 inactive
batches, 70 active batches and 2000 neutrons per batch. The
TWODANT results were
generated using S32 quadrature sets and inner and outer iteration
convergence criteria of 10-12.