


Next: Variance Reduction Using -scatter
Up: Correlated Sampling Technique
Previous: Correlated Sampling Technique
The correlated sampling technique described in the previous section assumes that
the actual simulation is done in the unperturbed system and the adjusting
weight
factors Fips (= 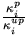 ) account for the
simulation of the correlated perturbed particles. The weight carried by the
perturbed particles would be a product of these adjusting weight factors
Fips. This requires that the adjusting weight factors for the correlated
game must always remain finite, which implies,
) account for the
simulation of the correlated perturbed particles. The weight carried by the
perturbed particles would be a product of these adjusting weight factors
Fips. This requires that the adjusting weight factors for the correlated
game must always remain finite, which implies,
|  |
(58) |
In some actual simulations these conditions may not be satisfied. For example,
in calculating perturbation effects due to voids, a particular phase-space
transition probability may vanish in the perturbed system but exist in the
unperturbed one. To account for this difficulty, a Monte Carlo perturbation
approach has been developed [Rie88] where the actual simulation is done in an
artificial reference system different from both the unperturbed and perturbed
systems. The probability density functions describing the transition process
in the reference system are a weighted mean of the probability density
functions of the unperturbed and perturbed systems. The important
characteristic of the reference system is that all particle reactions that can
take place in the unperturbed and perturbed systems will also have a non-zero
probability in the reference system. Thus, for example, a voided region would
not be admissible in the reference system if the unperturbed or perturbed
systems were not voided. However, the transpose is acceptable, i.e. one could
have a voided region in the perturbed system, in which case the weights would be
appropriately modified if a collision occurred in the ``voided'' region.
The responses for the unperturbed and
perturbed systems are calculated by correlating them to the reference
system's simulation. Also by the proper choice of the reference (ref) system,
it is
possible to avoid large fluctuations of the adjusting weight factors,
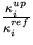 and
and 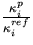 ,and reduce uncertainty of the differential effect.
The reference system [Maj94] may be chosen freely, but it also depends on
the type of
problem solved [Lux89]. Since the choice of the reference system will have an
effect on the variance, it may be subject to optimization methods[Lar95]. This
by
itself leads to a topic of future research. In appendix A,
some preliminary computational parametric studies are performed to observe
the effect of
different reference systems on the result of a perturbation problem. In this
research work, the arithmetic average of the parameters of the unperturbed and
perturbed systems has been used as the parameters for the reference system.
One of the requirements of the reference system is that
,and reduce uncertainty of the differential effect.
The reference system [Maj94] may be chosen freely, but it also depends on
the type of
problem solved [Lux89]. Since the choice of the reference system will have an
effect on the variance, it may be subject to optimization methods[Lar95]. This
by
itself leads to a topic of future research. In appendix A,
some preliminary computational parametric studies are performed to observe
the effect of
different reference systems on the result of a perturbation problem. In this
research work, the arithmetic average of the parameters of the unperturbed and
perturbed systems has been used as the parameters for the reference system.
One of the requirements of the reference system is that 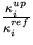 and
and 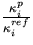 should be as
constant as possible. We will now explicitly derive the adjusting weight
factors for the unperturbed and perturbed systems and introduce the concept of
a
should be as
constant as possible. We will now explicitly derive the adjusting weight
factors for the unperturbed and perturbed systems and introduce the concept of
a 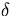 -scatter in the forward direction to avoid large fluctuations in the
adjusting weight factors.
-scatter in the forward direction to avoid large fluctuations in the
adjusting weight factors.
The cross sections for the reference, unperturbed
and perturbed systems are 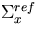 ,
, 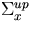 and
and 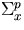 ,respectively, where x denotes a different cross section type. According to our
choice of the reference system, we have,
,respectively, where x denotes a different cross section type. According to our
choice of the reference system, we have,
| ![\begin{displaymath}
\Sigma_x^{ref} = \frac{1}{2}[\Sigma_x^{up} + \Sigma_x^p].\end{displaymath}](img143.gif) |
(59) |
The spatial collision distance, d, is sampled from
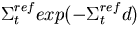 in the reference system. Then the
adjusting weight factors (WF) for the unperturbed and perturbed systems are
given by,
in the reference system. Then the
adjusting weight factors (WF) for the unperturbed and perturbed systems are
given by,
| ![\begin{displaymath}
WF^{up}=\frac{{\Sigma_t^{up}}exp(-\Sigma_t^{up}d)}
{{\Sigma_...
...a_t^{up}}{\Sigma_t^{ref}}exp
[(\Sigma_t^{ref}-\Sigma_t^{up})d],\end{displaymath}](img145.gif) |
(60) |
and
| ![\begin{displaymath}
WF^{p}=\frac{{\Sigma_t^{p}}exp(-\Sigma_t^{p}d)}
{{\Sigma_t^{...
...gma_t^{p}}{\Sigma_t^{ref}}exp
[(\Sigma_t^{ref}-\Sigma_t^{p})d],\end{displaymath}](img146.gif) |
(61) |
respectively. The weight which is carried along by the unperturbed and
perturbed particles is the product of these adjusting weight factors, WFup
and WFp, respectively.
Now, assuming 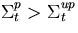 , the adjusting weight factor for the
unperturbed history has a positive exponent and may assume large values if d is
large. Similarly, the factor for the perturbed history may assume a very small
value. To avoid these large fluctuations, a
, the adjusting weight factor for the
unperturbed history has a positive exponent and may assume large values if d is
large. Similarly, the factor for the perturbed history may assume a very small
value. To avoid these large fluctuations, a 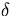 -scatter in the forward
direction is added to all three total cross sections [Rie88].
Introduction of a pseudo-collision with a
-scatter in the forward
direction is added to all three total cross sections [Rie88].
Introduction of a pseudo-collision with a 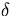 -scatter in the forward
direction increases the number of collisions without changing the expectation
values. For
each of these three cases the
-scatter in the forward
direction increases the number of collisions without changing the expectation
values. For
each of these three cases the 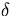 -scatter is chosen to yield the same
total cross section plus
-scatter is chosen to yield the same
total cross section plus 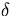 -scatter :
-scatter :
| 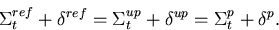 |
(62) |
Using these 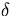 -scatters,
-scatters,
| ![\begin{displaymath}
WF^{up}=\frac{\Sigma_t^{up}+\delta^{up}}{\Sigma_t^{ref}+\del...
...p[(
\Sigma_t^{ref}+\delta^{ref}-\Sigma_t^{up}-\delta^{up})d]=1,\end{displaymath}](img149.gif) |
(63) |
and
| ![\begin{displaymath}
WF^{p}=\frac{\Sigma_t^{p}+\delta^{p}}{\Sigma_t^{ref}+\delta^...
...exp[(
\Sigma_t^{ref}+\delta^{ref}-\Sigma_t^{p}-\delta^{p})d]=1.\end{displaymath}](img150.gif) |
(64) |
Thus the large fluctuations in WFup and WFp are avoided. The
reference system's cross sections are chosen using equation (3.27) and a
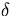 -scatter for the reference system (
-scatter for the reference system (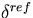 ) is selected.
Next equation
(3.30) can be used to determine the
) is selected.
Next equation
(3.30) can be used to determine the 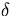 -scatters for the unperturbed and
perturbed systems.
-scatters for the unperturbed and
perturbed systems.



Next: Variance Reduction Using -scatter
Up: Correlated Sampling Technique
Previous: Correlated Sampling Technique
Amitava Majumdar
9/20/1999
![]() ) account for the
simulation of the correlated perturbed particles. The weight carried by the
perturbed particles would be a product of these adjusting weight factors
Fips. This requires that the adjusting weight factors for the correlated
game must always remain finite, which implies,
) account for the
simulation of the correlated perturbed particles. The weight carried by the
perturbed particles would be a product of these adjusting weight factors
Fips. This requires that the adjusting weight factors for the correlated
game must always remain finite, which implies,
![]() ,
, ![]() and
and ![]() ,respectively, where x denotes a different cross section type. According to our
choice of the reference system, we have,
,respectively, where x denotes a different cross section type. According to our
choice of the reference system, we have,
![\begin{displaymath}
WF^{up}=\frac{{\Sigma_t^{up}}exp(-\Sigma_t^{up}d)}
{{\Sigma_...
...a_t^{up}}{\Sigma_t^{ref}}exp
[(\Sigma_t^{ref}-\Sigma_t^{up})d],\end{displaymath}](img145.gif)
![\begin{displaymath}
WF^{p}=\frac{{\Sigma_t^{p}}exp(-\Sigma_t^{p}d)}
{{\Sigma_t^{...
...gma_t^{p}}{\Sigma_t^{ref}}exp
[(\Sigma_t^{ref}-\Sigma_t^{p})d],\end{displaymath}](img146.gif)
![]() , the adjusting weight factor for the
unperturbed history has a positive exponent and may assume large values if d is
large. Similarly, the factor for the perturbed history may assume a very small
value. To avoid these large fluctuations, a
, the adjusting weight factor for the
unperturbed history has a positive exponent and may assume large values if d is
large. Similarly, the factor for the perturbed history may assume a very small
value. To avoid these large fluctuations, a ![]() -scatter in the forward
direction is added to all three total cross sections [Rie88].
Introduction of a pseudo-collision with a
-scatter in the forward
direction is added to all three total cross sections [Rie88].
Introduction of a pseudo-collision with a ![]() -scatter in the forward
direction increases the number of collisions without changing the expectation
values. For
each of these three cases the
-scatter in the forward
direction increases the number of collisions without changing the expectation
values. For
each of these three cases the ![]() -scatter is chosen to yield the same
total cross section plus
-scatter is chosen to yield the same
total cross section plus ![]() -scatter :
-scatter :
![\begin{displaymath}
WF^{up}=\frac{\Sigma_t^{up}+\delta^{up}}{\Sigma_t^{ref}+\del...
...p[(
\Sigma_t^{ref}+\delta^{ref}-\Sigma_t^{up}-\delta^{up})d]=1,\end{displaymath}](img149.gif)
![\begin{displaymath}
WF^{p}=\frac{\Sigma_t^{p}+\delta^{p}}{\Sigma_t^{ref}+\delta^...
...exp[(
\Sigma_t^{ref}+\delta^{ref}-\Sigma_t^{p}-\delta^{p})d]=1.\end{displaymath}](img150.gif)