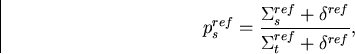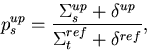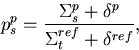Next: Correlated Sampling and Source
Up: Correlated Sampling Technique
Previous: Correlated Sampling in a
Variance reduction techniques can be applied to the reference system's
particles. We have applied survival biasing and Russian roulette [Lew93] to
the reference system's particles and correlated the unperturbed and perturbed
systems' particles to the reference system's particles. After determining the
site of collision, the survival chance of the reference system particle is
sampled from,
| 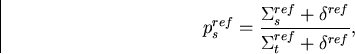 |
(65) |
where 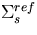 is the macroscopic scattering cross section of the
reference system. Next, the survival chance of the unperturbed and perturbed
particles are sampled from,
is the macroscopic scattering cross section of the
reference system. Next, the survival chance of the unperturbed and perturbed
particles are sampled from,
| 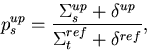 |
(66) |
and
| 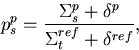 |
(67) |
respectively. The weights of the reference, unperturbed and perturbed
particles are modified at the site of the jth collision as follows,
|
Wjref = Wj-1refpsref,
|
(68) |
After the weight adjustment, Russian roulette is applied to the
reference system particles. In this procedure, one checks to determine if
the reference system particle weight has fallen below some minimum value,
in which case the reference system particle as well as
the unperturbed and perturbed particles are terminated. In this research work
we have simulated isotropically scattering systems. After each collision event
the new angular distribution for a
neutron is chosen isotropically.



Next: Correlated Sampling and Source
Up: Correlated Sampling Technique
Previous: Correlated Sampling in a
Amitava Majumdar
9/20/1999