Numerical Results

In this section, numerical results are given for different eigenvalue perturbation problems, utilizing the combined Monte Carlo CSFM method. The Monte Carlo ${\Delta}K$results are compared to that of the discrete ordinates code TWODANT [O'De82]. The TWODANT code is used to calculate the unperturbed and perturbed eigenvalues separately; these are then subtracted to determine ${\Delta}K$. The TWODANT code results for slab geometry are generated with the S₃₂ quadrature set and for X-Y geometry with the S₁₆ quadrature set. The inner and outer iteration convergence criteria are set to 10^-12. The cross sections of the reference systems for all test problems are chosen as the average of that of the unperturbed and perturbed systems. The percentage error given with all the results is calculated as follows:

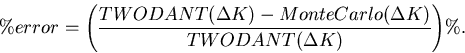$$\% error = {\left({\frac{TWODANT({\Delta}K) - Monte Carlo({\Delta}K)} {TWODANT({\Delta}K)}}\right)}\%.$$ (87)

Test Problem 1: heterogeneous slab, one energy group.
This case is a one energy group heterogeneous slab problem with vacuum boundary conditions on both ends. Dimensions and unperturbed cross sections for the slab are shown in figure 3.1. A perturbation is made in the 0.4 cm region in the middle. The ${\Delta}K$ results for two perturbations are shown in table 3.4 along with the corresponding TWODANT ${\Delta}K$s. The Monte Carlo runs utilize 140 active batches, 60 inactive batches and 8000 neutrons per batch. The standard deviation of the eigenvalue of the reference system is 0.71E-3 for the first problem of table 3.4.

 

Figure: Configuration of Heterogeneous Slab for Test Problem 1.

 

1|cHeterogeneous slab, 1c 1c T=6.0cm 1c|

$$\Sigma_t {\Sigma_{a}} \nu\Sigma_f {\le} {\le} {\le} {\le}$$ 1c|

$$\Sigma_t {\Sigma_{a}} \nu\Sigma_f$$ 1c all other X 1c 1c|

1|c|Perturbation in 1c|TWODANT 1c|Correlated 1c|error

$${\Delta}K {\Delta}K$$ 1|c| middle 0.4cm 1c|(%)

$$\Delta\Sigma_t \Delta\Sigma_a \mp$$ -0.019438 2.3

$${\Delta\Sigma}_s \; \delta^{ref}$$

$$\Delta\Sigma_t \Delta\Sigma_a \mp$$ -0.007613 1.4

$${\Delta\Sigma}_s \; \delta^{ref}$$

Test Problem 2a: homogeneous X-Y geometry, one energy group.
This case is a one energy group homogeneous X-Y geometry problem with vacuum boundary conditions on all sides. Dimensions and unperturbed cross sections for the problem are shown in figure 3.2. Cross section perturbations are made over the entire square region. The ${\Delta}K$ results for three different perturbations are shown in table 3.5, along with the corresponding TWODANT ${\Delta}K$s. The first Monte Carlo perturbation case utilizes 70 active batches, 30 inactive batches, and 2000 neutrons per batch, while the second and third cases utilize 70 active batches, 30 inactive batches, and 4000 neutrons per batch.

 

Figure: Configurations of X-Y geometry for Test Problems 2a and 2b.

 

$$\Sigma_t$$ 1|cUnperturbed 1ccross-sections 1c|

$$\Sigma_s {\Sigma_{a}} \nu\Sigma_f$$ 1c|

1|c|Perturbed 1|c|TWODANT 1|c|Correlated 1|c|error

$${\Delta}K {\Delta}K$$ 1|c| cross-sections 1|c|(%)

$${\Delta\nu\Sigma}_f \mp$$ -0.016475 .04

$$\; \delta^{ref}$$

$$\Delta\Sigma_t \Delta\Sigma_a \mp$$ -0.0072755 1.7

$$\; \delta^{ref}$$

$$\Delta\Sigma_t \Delta\Sigma_a {\pm}$$ 0.005958 1.8

$${\Delta\Sigma}_s {\Delta\nu\Sigma}_f \delta^{ref}$$

Test Problem 2b: heterogeneous X-Y geometry, one energy group.
This case is a one energy group heterogeneous X-Y geometry problem with vacuum boundary conditions on all sides. Dimensions and unperturbed cross sections for the problem are shown in figure 3.2. Cross section perturbations are made in the middle square region. The ${\Delta}K$ results for three different perturbations are shown in table 3.6, along with the corresponding TWODANT ${\Delta}K$s. The first Monte Carlo perturbation case utilizes 70 active batches, 30 inactive batches and 4000 neutrons per batch, while the second and third Monte Carlo perturbation case employ 100 active batches, 40 inactive batches and 4000 neutrons per batch.

 

$$\Sigma_t$$ 1|cUnperturbed 1ccross-sections 1c|

$$\Sigma_s {\Sigma_{a}} \nu\Sigma_f$$ 1c|

1|c|Perturbed 1|c|TWODANT 1|c|Correlated 1|c|error

$${\Delta}K {\Delta}K$$ 1|c| cross-sections 1|c|(%)

$${\Delta\nu\Sigma}_f {\pm}$$ 0.0044562 1.8

$$\; \delta^{ref}$$

$$\Delta\Sigma_t \Delta\Sigma_a \mp$$ -0.0044909 3.0

$$\; \delta^{ref}$$

$$\Delta\Sigma_t \Delta\Sigma_a {\pm}$$ 0.003884 2.6

$${\Delta\Sigma}_s {\Delta\nu\Sigma}_f \delta^{ref}$$

Test Problem 3a: homogeneous X-Y geometry, two energy group.
This case is a two energy group homogeneous X-Y geometry (10 cm X 10 cm) problem with vacuum boundary conditions on all sides. Cross section perturbations are done over the whole square region. Unperturbed and perturbed cross sections and ${\Delta}K$ results for a perturbation case is shown in table 3.7 along with the TWODANT ${\Delta}K$s. The Monte Carlo perturbation case has 110 active batches, 30 inactive batches and 2000 neutrons per batch.

 

1|cUnperturbed 1ccross-sections 1c 1c|

$${\Sigma}_{t1} {\nu\Sigma}_{f1} {\Sigma}_{s11} {\Sigma}_{s12}$$

$${\Sigma}_{t2} {\nu\Sigma}_{f2} {\Sigma}_{s21} {\Sigma}_{s22}$$

1|c|Perturbed 1|c|TWODANT 1|c| Correlated 1|c|error

$${\Delta}K {\Delta}K$$ 1|c| cross-sections 1|c|(%)

$${\Delta\Sigma}_{t1} {\Delta\Sigma_{a1}=.001} {\pm}$$ 0.122134 0.5

$$\delta^{ref}$$

Test Problem 3b: Millstone Reactor Assembly.
This problem is a 10 cm X 10 cm square region with reflecting boundary conditions on all sides. The unperturbed cross section correspond to a Millstone [NRC85] reactor fuel assembly with 2.9 weight percent (w/o) enrichment, without burnable poison (bp) pins at hot full power condition with 1398 ppm critical boron concentration, while the perturbed cross section correspond to a 2.9 w/o, 20 burnable poison assembly at the same conditions. These cross sections were generated using the CPM-2 [Jon87] code. Cross section perturbations are made over the entire square region. The cross sections are given in table 3.8 and the ${\Delta}K$ result is given in table 3.9. The Monte Carlo run utilizes 140 active batches, 60 inactive batches, and 6000 neutrons per batch. The standard deviation of the reference system eigenvalue is 0.16E-3.

 

1|c 1c 1c 1c|

$${\Sigma}_{t1} {\nu\Sigma}_{f1} {\Sigma}_{s11} {\Sigma}_{s12}$$

$${\Sigma}_{t2} {\nu\Sigma}_{f2} {\Sigma}_{s21} {\Sigma}_{s22}$$

1|c 1c 1c 1c|

1|c 1c 1c 1c|

$${\Sigma}_{t1} {\nu\Sigma}_{f1} {\Sigma}_{s11} {\Sigma}_{s12}$$

$${\Sigma}_{t2} {\nu\Sigma}_{f2} {\Sigma}_{s21} {\Sigma}_{s22}$$

1|c 1c 1c 1c|

 

1|c|TWODANT 1|c| Correlated 1|c|error

$${\Delta}K {\Delta}K$$ 1|c|(%)

$$\; \; \;$$

$$-0.159771\mp$$ -0.165136 3.2

$$\; \delta^{ref1} \delta^{ref2} \;$$

Test Problem 4: variation of test problem 1.
This is the same as test problem 1, except that the 0.4 cm region of moderator in the middle is replaced with an absorber. Unperturbed cross sections of the absorber are $\Sigma_t$ = 5.0 cm^-1, and $\Sigma_s$ = 0.1 cm^-1. Perturbed cross sections of the absorber are $\Sigma_t$ = 5.0 cm^-1, and $\Sigma_s$ = 0.3 cm^-1. The results are shown in table 3.10. The Monte Carlo runs utilize 140 active batches, 60 inactive batches and 8000 neutrons per batch.

 

1|cHeterogeneous slab, 1c 1c T=6.0cm 1c|

$$\Sigma_t {\Sigma_{a}} \nu\Sigma_f {\le} {\le} {\le} {\le}$$ 1c|

$$\Sigma_t {\Sigma_{a}} \nu\Sigma_f {\le} {\le}$$ 1c 1c|

$$\Sigma_t {\Sigma_{a}} \nu\Sigma_f$$ 1c all other X 1c 1c|

1|c|Perturbation in 1c|TWODANT 1c|Correlated 1c|error

$${\Delta}K {\Delta}K$$ 1|c| middle 0.4cm 1c|(%)

$$\Delta\Sigma_a {\Delta\Sigma}_s \mp$$ 0.00031 13.7

$$\; \delta^{ref}$$

Test Problem 5: source convergence problem.
This test problem specifically looks into the case where the shapes of the unperturbed and perturbed scalar fluxes are significantly different. The unperturbed problem is a 16 mfp one group homogeneous slab with $\Sigma_t$ = 1.0, $\Sigma_s$ = 0.9, and $\nu\Sigma_f$ = 0.11 and vacuum boundary conditions on both ends. For the perturbed problem the middle 4 cm region of the slab is replaced with a material representing moderator with $\Sigma_t$ = 2.35, $\Sigma_s$ = 2.3, and $\nu\Sigma_f$ = 0.0. The perturbed and unperturbed scalar fluxes from TWODANT are shown in figure 3.3.

 

Figure: Perturbed and Unperturbed Scalar Fluxes from TWODANT.

Results of TWODANT and CSFM Monte Carlo $\Delta$Ks are shown in table 3.11. The Monte Carlo case has 140 active batches, 60 inactive batches and 8000 neutrons per batch.

 

1|c|TWODANT 1|c| Correlated 1|c|error

$${\Delta}K {\Delta}K$$ 1|c|(%)

$$\; \; \;$$

$$\mp$$ -0.168909 1.2

$$\; \delta^{ref} \;$$