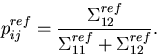Multigroup Energy Transfer

For energy dependent problems with multigroup cross sections, the scattering matrix for the reference system may be determined by taking the average of the unperturbed and perturbed scattering matrices. For example, suppose the scattering matrices for the unperturbed and perturbed systems are given respectively by,

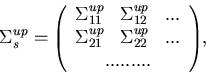$${\Sigma_s^{up}} = {\left(\begin{array} {ccc}\Sigma_{11}^{up}... ...\;\;\Sigma_{22}^{up}\;\;\;...\\ .........\end{array} \right)},$$ (83)

and

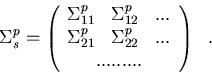$$\;\;\; {\Sigma_s^{p}} = {\left(\begin{array} {ccc}\Sigma_{11... ...Sigma_{22}^{p}\;\;\;...\\ .........\end{array} \right)\;\;\;}.$$ (84)

Then the scattering matrix for the reference system is,

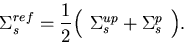$${\Sigma_s^{ref}} = {{1}\over{2}} {\left(\begin{array} {c} {{\Sigma_{s}^{up}+{\Sigma_{s}^{p}}}} \end{array}\right)}.$$ (85)

For multigroup problems, survival biasing is applied at the site of the collision to the reference, unperturbed and perturbed particles as explained in section 3.3.2. Then the reference scattering matrix is used to determine the outgoing energy group of the reference particle, using the probability of a reference particle to scatter from energy group i to j :

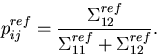$$p_{ij}^{ref} = \frac{\Sigma_{12}^{ref}}{\Sigma_{11}^{ref}+\Sigma_{12}^{ref}}.$$ (86)

The unperturbed and perturbed particles are constrained to follow the same energy group transfer as the reference particle.