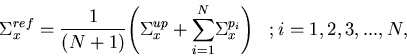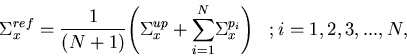Next: Forward -scatter
Up: Multiple Reactivity Calculation
Previous: Multiple Reactivity Calculation
We have chosen to define the reference system by,
| 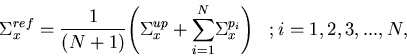 |
(89) |
where x denotes
a different cross section type. It is possible to choose a different
reference
system; the optimum choice may vary from one problem
to another. For all the numerical results shown in this chapter we have used
equation (4.2) to determine the reference system. The Monte Carlo
particle tracking is done in this
reference system. The distance to collision d is sampled from
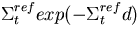 . The adjusting weight factors for the
unperturbed and all perturbed systems are then given respectively by,
. The adjusting weight factors for the
unperturbed and all perturbed systems are then given respectively by,
| 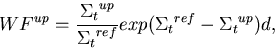 |
(90) |
and
| 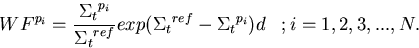 |
(91) |
Amitava Majumdar
9/20/1999