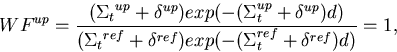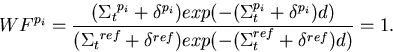Next: K Calculation
Up: Multiple Reactivity Calculation
Previous: Reference System
As with the single perturbation case, a 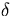 -scatter cross section
is added to the total cross sections of the reference,
unperturbed and perturbed systems. The
-scatter cross section
is added to the total cross sections of the reference,
unperturbed and perturbed systems. The 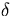 -scatter cross section
for the
reference system (
-scatter cross section
for the
reference system (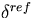 ) is chosen, depending upon the problem, such
that,
) is chosen, depending upon the problem, such
that,
| 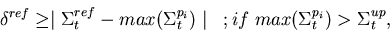 |
(92) |
or,
| 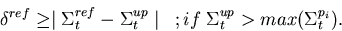 |
(93) |
The 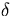 -scatter cross section for the unperturbed system (
-scatter cross section for the unperturbed system (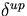 )
and perturbed
systems (
)
and perturbed
systems (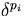 , i = 1,2,3,...,N) are chosen as,
, i = 1,2,3,...,N) are chosen as,
| 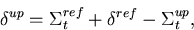 |
(94) |
and,
| 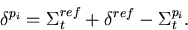 |
(95) |
The conditions imposed by equation (4.5) and (4.6)
ensure that all the 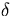 -scatter cross sections are nonnegative.
In our test problems the above four equations are used to
determine forward
-scatter cross sections are nonnegative.
In our test problems the above four equations are used to
determine forward 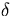 -scatters for the reference, unperturbed and all perturbed
systems. The distance to collision
d in the reference system is sampled from
-scatters for the reference, unperturbed and all perturbed
systems. The distance to collision
d in the reference system is sampled from
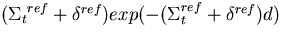 , and
the modified biasing factors for the unperturbed and all perturbed systems
become,
, and
the modified biasing factors for the unperturbed and all perturbed systems
become,
| 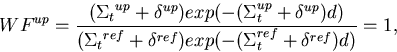 |
(96) |
and,
| 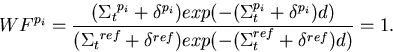 |
(97) |
This avoids large fluctuations in WFup and WFpi.



Next: K Calculation
Up: Multiple Reactivity Calculation
Previous: Reference System
Amitava Majumdar
9/20/1999
![]() -scatter cross section
is added to the total cross sections of the reference,
unperturbed and perturbed systems. The
-scatter cross section
is added to the total cross sections of the reference,
unperturbed and perturbed systems. The ![]() -scatter cross section
for the
reference system (
-scatter cross section
for the
reference system (![]() ) is chosen, depending upon the problem, such
that,
) is chosen, depending upon the problem, such
that,