$\Delta$K Calculation

All of the simulation procedures described in section 3.3.4 and 3.3.5 apply to multiple $\Delta$K calculation and hence will not be repeated here. Only the additional computations necessary for multiple $\Delta$K calculation will be described in this section. Instead of a single weight adjusting factor W^p for a single perturbed system, now we have multiple weight adjusting factors, W^p_is (i=1,2,...,N), for the multiple perturbed systems. For the first fission generation, the starting weights of all the perturbed particles are set to unity. For the fission matrix eigenvalue calculation in the reference system, the first generation is started with an assumed source distribution and W^ref = 1, where W^ref is the weight of a reference system particle. During the random walk simulation, the weight of each perturbed particle is modified by multiplying them with an appropriate adjusting weight factor WF^p_i.

The fission matrix elements for the perturbed fission matrix, A^p_i, is scored as,

$${a_{l,m}^{p_i}}={a_{l,m}^{p_i}} + W^{p_i}{[{\nu^{p_i}\Sigma... ...}] \over{[\Sigma_t^{ref} + \delta^{ref}]}}\;\;\;;i=1,2,3,...N.$$ (98)

The dominant eigenvalues K^ref, K^up and K^p_i of matrices A^ref, A^up and A^p_i respectively, are determined numerically. Then, multiple $\Delta$Ks due to multiple perturbations (p_i, i = 1,2,3,...,N) are calculated as,

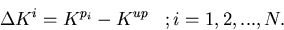$$\Delta{K}^i = K^{p_i} - K^{up}\;\;\;; i = 1,2,...,N.$$ (99)

Biasing factors for variance reduction of all the perturbed particles are:

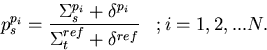$$p_s^{p_i} = {{\Sigma_s^{p_i} + \delta^{p_i}}\over{\Sigma_t^{ref} + \delta^{ref}}}\;\;\;; i = 1,2,...N.$$ (100)

The weights of all the perturbed particles are reduced as follows at the site of the j^th collision,

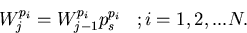$$W_j^{p_i} = W_{j-1}^{p_i}p_s^{p_i}\;\;\;; i = 1,2,...N.$$ (101)

For multigroup problems, the scattering matrix of the reference system is,

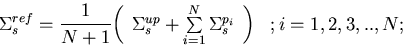$${\Sigma_s^{ref}} = {{1}\over{N+1}} {\left(\begin{array} {c} ... ...gma_{s}^{p_i}}}}} \end{array}\right)}\;\;\;; i = 1,2,3,..,N;$$ (102)

where,

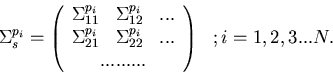$$\;\;\; {\Sigma_s^{p_i}} = {\left(\begin{array} {ccc}\Sigma_{... ...;\;\;...\\ .........\end{array} \right)\;\;\;}; i = 1,2,3...N.$$ (103)

For multigroup problems, survival biasing is applied to the reference, unperturbed and all perturbed particles. Then the unperturbed and all perturbed particles follow the same energy group transfer as the reference particle.