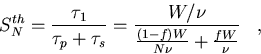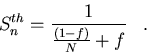Next: Parallelization on the CRAY
Up: Parallel Photon Transport Algorithm
Previous: Parallel Photon Transport Algorithm
The principal measure of parallelization efficiency is the speedup, SN,
defined
to be the ratio of the time to execute the computational workload W
on a single
processor to the time on N processors,
| 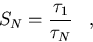 |
(104) |
where 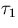 is the time to execute the workload on a single processor
and
is the time to execute the workload on a single processor
and 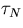 is the time to execute the workload on N processors.
is the time to execute the workload on N processors.
The time 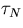 is the sum of three terms,
is the sum of three terms,
| 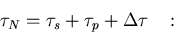 |
(105) |
(1) the time 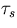 to execute the serial portion of the workload, (2) the
time
to execute the serial portion of the workload, (2) the
time
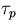 to execute the parallel portion, and (3) an additional time
to execute the parallel portion, and (3) an additional time
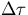 due to the parallelization overhead which is quite general and accounts for any
overhead due to implementing the algorithm on the parallel processor, either
due
to the hardware, the network, the operating system, or the algorithm. We would
expect it to be a function of the number of processors, N, as well as the
workload, W,
due to the parallelization overhead which is quite general and accounts for any
overhead due to implementing the algorithm on the parallel processor, either
due
to the hardware, the network, the operating system, or the algorithm. We would
expect it to be a function of the number of processors, N, as well as the
workload, W,
| 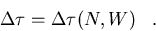 |
(106) |
The theoretical speedup, SNth, is the speedup assuming zero
parallelization
overhead,
| 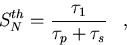 |
(107) |
which can be compared to the true speedup:
| 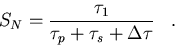 |
(108) |
Note that the theoretical speedup is the best that can be achieved. The ratio
of
the true speedup to the theoretical speedup is the parallelization efficiency,
| 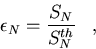 |
(109) |
which is a measure of the efficiency of the parallel processor to execute a
given
parallel algorithm. Any degradation in performance due to parallelization
overhead will result in 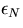 being less than one.
being less than one.
Now we introduce the serial fraction f,
| 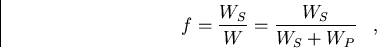 |
(110) |
where W is the total computational workload, consisting of the serial workload
WS, and the parallel workload Wp, which can by definition be performed
on N processors. We define W in arbitrary units of
workload and assume the processor speed is 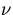 (workload unit per second),
which leads to the following expression for the theoretical speedup,
(workload unit per second),
which leads to the following expression for the theoretical speedup,
| 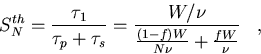 |
(111) |
or
| 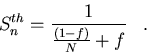 |
(112) |
For Monte Carlo [Mar93], the total workload for the single processor
cases (N=1) can be
approximated very well (as will be seen by our timing results) by a simple
linear function of the number of histories, Nh, to be simulated:
| 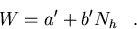 |
(113) |
Now we divide equation (5.10) by 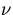 , which is a constant for a specific
processor and define new constants a and b to obtain the single processor
execution time:
, which is a constant for a specific
processor and define new constants a and b to obtain the single processor
execution time:
| 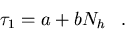 |
(114) |
Since all histories are independent, they can be tracked in parallel.
Further, it
is reasonable to associate the constant a with the serial time, 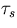 .
The
serial fraction is given by,
.
The
serial fraction is given by,
| 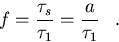 |
(115) |
Therefore, one can find the constants a and b by observing at least two
different workloads (i.e. different Nh) for the N=1 (single processor)
case.



Next: Parallelization on the CRAY
Up: Parallel Photon Transport Algorithm
Previous: Parallel Photon Transport Algorithm
Amitava Majumdar
9/20/1999
![]() is the sum of three terms,
is the sum of three terms,