Parallel Algorithm

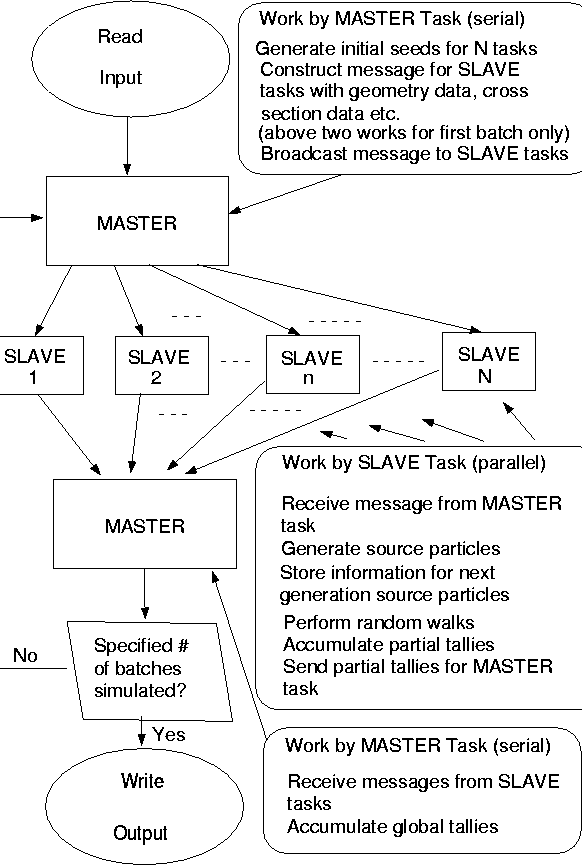
The eigenvalue and perturbation parallel algorithms are also based on a master-slave approach, as described in section 5.2. The master processor divides the total number of particles, for each fission generation, equally among all the available processors or slaves. Each slave processor simulates random walk for particle histories simultaneously with other slave processors. This simultaneous simulation of particle histories among all the slave processors is possible because particle histories are independent within each fission generation. Each slave processor also stores the sites and the number of next generation fission neutrons produced. This information is used by each slave processor for the next fission generation. At the end of each fission

 

Figure: Flow Diagram for Eigenvalue and $\Delta$K Parallel Monte Carlo Algorithms.

generation, tally results from each slave processor are collected in the master processor and the eigenvalue is computed. This iteration procedure, over fission generations, is repeated several times. This parallel algorithm also obeys the principle of reproducibility. Independent and reproducible sequences of random numbers are generated using the EGS4 [Nel85] random number generator. Each processor is given its own random number seed. These seeds are generated using the skip ahead approach, which allows each processor to generate a sequence of random numbers not overlapping with any other processor's random number sequence.