


Next: IBM-SP2 Parallel Computer
Up: Parallel Monte Carlo Eigenvalue
Previous: Parallel Algorithm
Similar to section 5.2.1, an expression for speedup can be derived for the
eigenvalue and perturbation parallel algorithms.
For the master-slave algorithm, serial communication takes place, because the
master process can only receive one message at a time. We expect the
parallelization overhead and synchronization time to be proportional to (N-1).
Hence, we
express 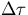 as;
as;
| 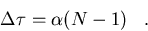 |
(124) |
The time for a parallel
simulation on N processors can be written as;
| 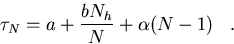 |
(125) |
In the above equation, after evaluating constants a and b from two serial
execution time, all the terms are known except 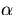 . The parameter
. The parameter
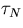 is the
actual measured time on N processors of IBM-SP2. Hence,
is the
actual measured time on N processors of IBM-SP2. Hence, 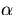 can be
determined from equation (5.22). The observed speedup is expressed as;
can be
determined from equation (5.22). The observed speedup is expressed as;
| 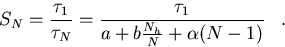 |
(126) |
The predicted speedup follows the curve given by;
| 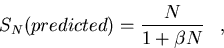 |
(127) |
where,
| 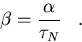 |
(128) |
Here  represents the fraction of total computation time spent in
parallelization overhead, communication, synchronization,
etc. between two processors [Mat94].
represents the fraction of total computation time spent in
parallelization overhead, communication, synchronization,
etc. between two processors [Mat94].



Next: IBM-SP2 Parallel Computer
Up: Parallel Monte Carlo Eigenvalue
Previous: Parallel Algorithm
Amitava Majumdar
9/20/1999
![]() as;
as;