


Next: CONCLUSIONS AND FUTURE WORK
Up: Parallel Monte Carlo Eigenvalue
Previous: Results
The values of 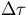 s for the IBM-SP2 computer was calculated from equation
(5.22) where
s for the IBM-SP2 computer was calculated from equation
(5.22) where 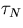 is the actual wall clock timing on N processors. In
tables
5.10, 5.11, 5.12 and 5.13 we show the
is the actual wall clock timing on N processors. In
tables
5.10, 5.11, 5.12 and 5.13 we show the 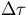 s corresponding to results of
tables 5.6, 5.7, 5.8 and 5.9 respectively.
s corresponding to results of
tables 5.6, 5.7, 5.8 and 5.9 respectively.
Table:
IBM-SP2 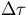 s for 8000p/b, 100 batch case.
s for 8000p/b, 100 batch case.
| 1|c|# of processors |
1|c| Source Iteration |
1|c| Fission Matrix |
1c| Correlated Sampling |
| 2 |
29.2 |
6.58 |
15.0 |
| 4 |
10.0 |
11.4 |
26.4 |
| 8 |
12.5 |
15.1 |
30.8 |
| 10 |
13.7 |
20.9 |
27.9 |
Table:
IBM-SP2 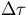 s for 16000p/b, 100 batch case.
s for 16000p/b, 100 batch case.
| 1|c|# of processors |
1|c| Source Iteration |
1|c| Fission Matrix |
1c| Correlated Sampling |
| 2 |
11.4 |
14.4 |
62.8 |
| 4 |
17.3 |
13.0 |
16.3 |
| 8 |
15.7 |
18.7 |
33.9 |
| 10 |
24.6 |
18.3 |
45.0 |
Table:
IBM-SP2 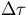 s for 16000p/b, 50 batch case.
s for 16000p/b, 50 batch case.
| 1|c|# of processors |
1|c| Source Iteration |
1|c| Fission Matrix |
1c| Correlated Sampling |
| 2 |
4.4 |
18.3 |
13.1 |
| 4 |
6.9 |
9.9 |
9.3 |
| 8 |
7.7 |
6.1 |
11.9 |
| 10 |
8.4 |
8.6 |
17.1 |
Table:
IBM-SP2 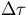 s for 32000p/b, 50 batch case.
s for 32000p/b, 50 batch case.
| 1|c|# of processors |
1|c| Source Iteration |
1|c| Fission Matrix |
1c| Correlated Sampling |
| 2 |
6.4 |
6.5 |
22.8 |
| 4 |
9.6 |
14.4 |
20.3 |
| 8 |
12.9 |
8.4 |
25.7 |
| 10 |
10.6 |
11.0 |
17.5 |
Even though it is difficult to predict an
empirical formula that exactly determines
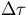 s, we notice that for most of the cases
s, we notice that for most of the cases 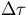 is about a
constant. If
is about a
constant. If 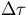 is assumed to be a constant then
is assumed to be a constant then 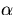 is
proportional to
is
proportional to 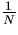 . Hence speedup models for IBM-SP2 can be
predicted reasonably well with two parameters, the serial time constant a and the
proportionality constant for
. Hence speedup models for IBM-SP2 can be
predicted reasonably well with two parameters, the serial time constant a and the
proportionality constant for 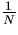 .
.



Next: CONCLUSIONS AND FUTURE WORK
Up: Parallel Monte Carlo Eigenvalue
Previous: Results
Amitava Majumdar
9/20/1999
![]() s for the IBM-SP2 computer was calculated from equation
(5.22) where
s for the IBM-SP2 computer was calculated from equation
(5.22) where ![]() is the actual wall clock timing on N processors. In
tables
5.10, 5.11, 5.12 and 5.13 we show the
is the actual wall clock timing on N processors. In
tables
5.10, 5.11, 5.12 and 5.13 we show the ![]() s corresponding to results of
tables 5.6, 5.7, 5.8 and 5.9 respectively.
s corresponding to results of
tables 5.6, 5.7, 5.8 and 5.9 respectively.
![]() s, we notice that for most of the cases
s, we notice that for most of the cases ![]() is about a
constant. If
is about a
constant. If ![]() is assumed to be a constant then
is assumed to be a constant then ![]() is
proportional to
is
proportional to ![]() . Hence speedup models for IBM-SP2 can be
predicted reasonably well with two parameters, the serial time constant a and the
proportionality constant for
. Hence speedup models for IBM-SP2 can be
predicted reasonably well with two parameters, the serial time constant a and the
proportionality constant for ![]() .
.