next up previous
Next: for the IBM-SP2 Up: Parallel Monte Carlo Eigenvalue Previous: IBM-SP2 Parallel Computer

Results

We have measured parallel speedups for three different algorithms. The first and second algorithms calculate eigenvalues using the source iteration technique and the fission matrix approach, respectively. The third algorithm calculates $\Delta$K using the correlated sampling technique applied to the fission matrix approach of eigenvalue calculation (two $\Delta$Ks are calculated from a single Monte Carlo simulation). The amount of communication (measured within the master processor) between the master and the slave processors is largest for the perturbation algorithm and smallest for the source iteration eigenvalue algorithm. The number of communications required per iteration for the source iteration algorithm is three, for the fission matrix algorithm is four, and for the reactivity algorithm is eight. Table 5.5 shows the constants a and b for the three algorithms. In tables 5.6, 5.7, 5.8 and 5.9 we show wall-clock timing results for different cases (i.e., number of particles/batch (p/b) and number of batches (b)) on the IBM-SP2 for the three different algorithms. Figures 5.6 and 5.7 show observed and predicted speedup results for the source iteration eigenvalue calculation. Figure 5.8 shows the percentage of total computation time spent in communication (message passing) in the master processor for the source iteration algorithm. Figures 5.9, 5.10, and 5.11 show similar plots for fission matrix eigenvalue calculations and figures 5.12, 5.13 and 5.14 show plots for correlated sampling perturbation calculations. We find that our predicted speedup results match the observed results reasonably well. The observed results were taken on the dedicated IBM-SP2 parallel computer. From the speedup plots, we see that we obtain speedups close to 9 for 10 processors for all the three algorithms. Among these three algorithms, the perturbation algorithm shows largest fraction of total computation time spent in communication.

 
Table: Constants a and b of single processor execution time.
1|c|Algorithm type 1|c| a (sec) 1c| b (sec/history)
Source Iteration Eigenvalue 0.5194 4.5692E-4
Fission Matrix Eigenvalue 0.02 4.434E-4
Correlated Sampling Reactivity 0.7431 6.5815E-4










 
Table: Wall-clock Timing Results on IBM-SP2 for 8000 particle/batch, 100 batch case.
# of 3|c|Wall-clock timings in seconds    
1|c| processors 1|c|Source Iteration 1|c|Fission Matrix 1c|Correlated Sampling
1 365.84 357.52 527.59
2 212.23 183.96 279.25
4 105.24 100.11 158.92
8 58.72 59.51 97.61
10 50.73 56.39 81.55



 
Table: Wall-clock Timing Results on IBM-SP2 for 16000 particle/batch, 100 batch case.
# of 3|c|Wall-clock timings in seconds    
1|c|processors 1|c|Source Iteration 1|c|Fission Matrix 1c|Correlated Sampling
1 731.73 710.94 1053.57
2 377.43 369.10 590.04
4 200.64 190.38 280.29
8 107.58 107.40 166.28
10 98.18 89.30 151.37


 
Table: Wall-clock Timing Results on IBM-SP2 for 16000 particle/batch, 50 batch case.
# of 3|c|Wall-clock timings in seconds    
1|c|processors 1|c|Source Iteration 1|c|Fission Matrix 1c|Correlated Sampling
1 364.36 354.04 526.03
2 187.65 195.72 277.08
4 98.82 98.59 141.53
8 53.78 50.44 78.39
10 45.47 44.10 70.20


 
Table: Wall-clock Timing Results on IBM-SP2 for 32000 particle/batch, 50 batch case.
# of 3|c|Wall-clock timings in seconds    
1|c|processors 1|c|Source Iteration 1|c|Fission Matrix 1c|Correlated Sampling
1 729.08 709.55 1050.06
2 372.50 361.28 550.08
4 192.92 191.80 284.25
8 104.75 97.13 158.12
10 84.29 82.02 123.57





 
Figure: Source Iteration Speedup Plots.
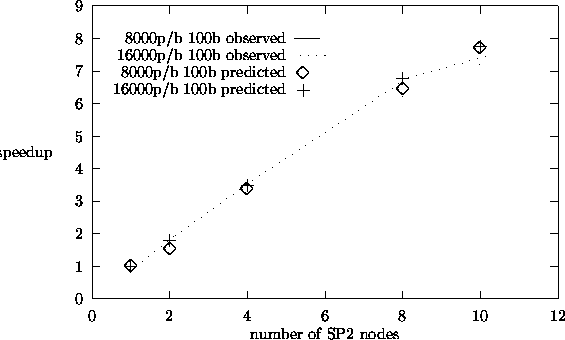\begin{figure} \begin{center} \setlength {\unitlength}{0.240900pt} \ifx\plotp... ...0){$+$}} \put(1233,773){\makebox(0,0){$+$}}\end{picture}\end{center}\end{figure}


 
Figure: Source Iteration Speedup Plots.
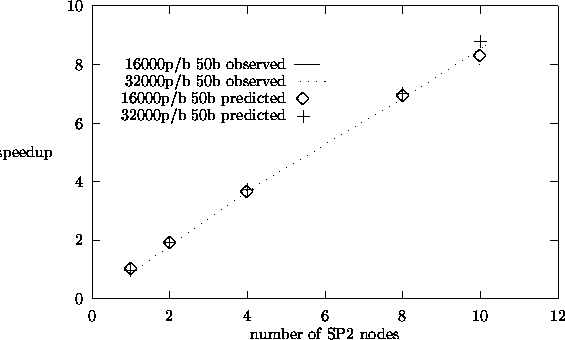\begin{figure} \begin{center} \setlength {\unitlength}{0.240900pt} \ifx\plotp... ...0){$+$}} \put(1233,785){\makebox(0,0){$+$}}\end{picture}\end{center}\end{figure}




 
Figure: % of Total Time Spent in Communication in a Processor for Source Iteration.
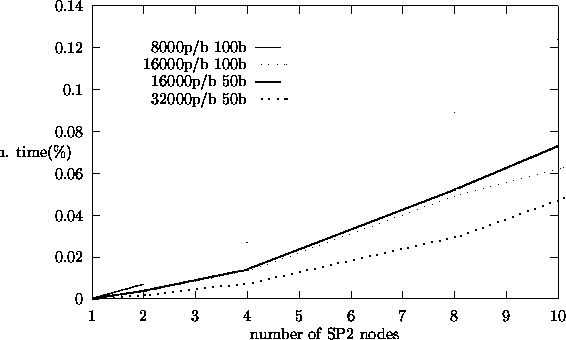\begin{figure} \begin{center} \setlength {\unitlength}{0.240900pt} \ifx\plotp... ...t} } \put(1436,375){ \usebox {\plotpoint} }\end{picture}\end{center}\end{figure}




 
Figure: Fission Matrix Speedup Plots.
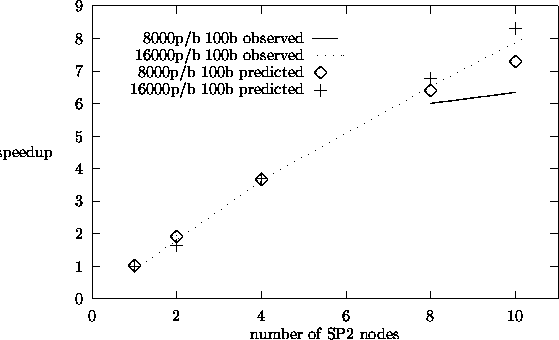\begin{figure} \begin{center} \setlength {\unitlength}{0.240900pt} \ifx\plotp... ...0){$+$}} \put(1325,818){\makebox(0,0){$+$}}\end{picture}\end{center}\end{figure}




 
Figure: Fission Matrix Speedup Plots.
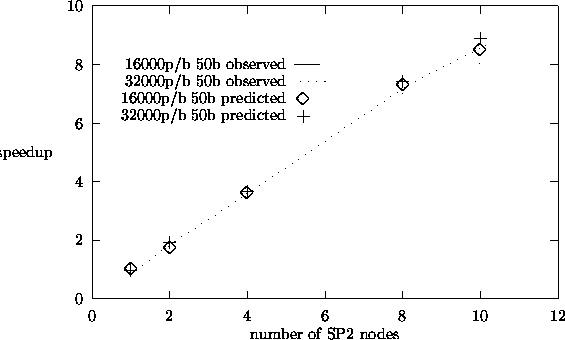\begin{figure} \begin{center} \setlength {\unitlength}{0.240900pt} \ifx\plotp... ...0){$+$}} \put(1233,793){\makebox(0,0){$+$}}\end{picture}\end{center}\end{figure}




 
Figure: % of Total Time Spent in Communication in a Processor for Fission Matrix.
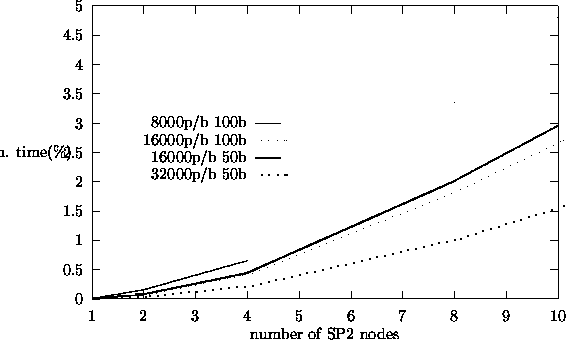\begin{figure} \begin{center} \setlength {\unitlength}{0.240900pt} \ifx\plotp... ...t} } \put(1436,354){ \usebox {\plotpoint} }\end{picture}\end{center}\end{figure}




 
Figure: Correlated Sampling Speedup Plots.
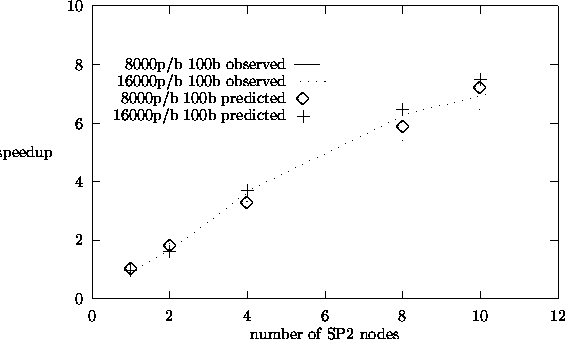\begin{figure} \begin{center} \setlength {\unitlength}{0.240900pt} \ifx\plotp... ...0){$+$}} \put(1233,686){\makebox(0,0){$+$}}\end{picture}\end{center}\end{figure}




 
Figure: Correlated Sampling Speedup Plots.
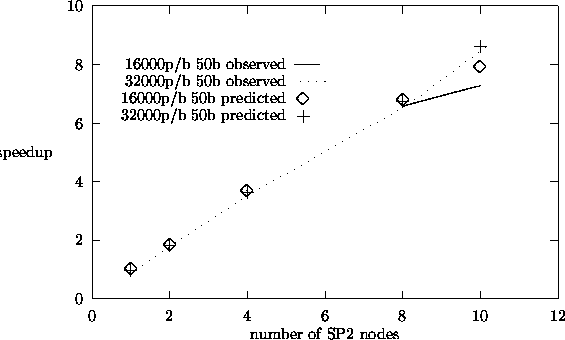\begin{figure} \begin{center} \setlength {\unitlength}{0.240900pt} \ifx\plotp... ...0){$+$}} \put(1233,772){\makebox(0,0){$+$}}\end{picture}\end{center}\end{figure}




 
Figure: % of Total Time Spent in Communication in a Processor for Correlated Sampling.
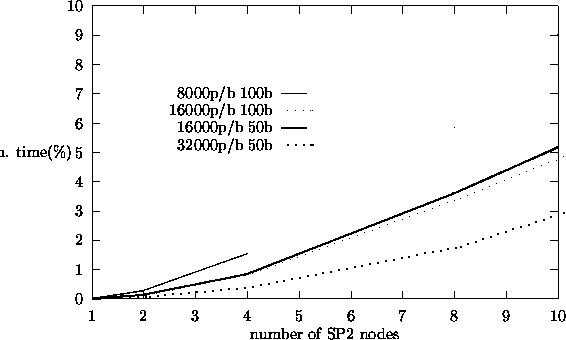\begin{figure} \begin{center} \setlength {\unitlength}{0.240900pt} \ifx\plotp... ...t} } \put(1436,337){ \usebox {\plotpoint} }\end{picture}\end{center}\end{figure}

next up previous
Next: for the IBM-SP2 Up: Parallel Monte Carlo Eigenvalue Previous: IBM-SP2 Parallel Computer
Amitava Majumdar
9/20/1999