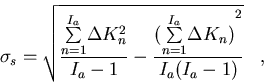Next: Correlated Sampling Fission Matrix
Up: Correlated Sampling Technique
Previous: Variance Reduction Using -scatter
Most Monte Carlo codes determine the eigenvalue of a system by the source
iteration method. Application of the source iteration method encounters
difficulties when used to calculate eigenvalue perturbations because
perturbed weights are propagated
from one generation to another. Experience has shown [Rie89, Rie84, Gal95]
that the statistical fluctuations in the propagated weights grow considerably,
and for most cases any useful information regarding the
perturbation is lost over many
generations. We have solved the same problems given in table 3.1 by applying
the correlated sampling technique to the source iteration method of eigenvalue
calculation.
The actual Monte Carlo simulation is done in the reference system,
with cross sections determined as the average of the unperturbed and
perturbed systems. As discussed earlier, a
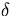 -scatter cross section is added to the total cross section for each
of the reference,
unperturbed, and perturbed systems to avoid fluctuations in the adjusting
weight
factors. For illustration, the value of
-scatter cross section is added to the total cross section for each
of the reference,
unperturbed, and perturbed systems to avoid fluctuations in the adjusting
weight
factors. For illustration, the value of 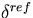 is given
along with the perturbation results
in table 3.2. The standard deviation of a single generation
is given
along with the perturbation results
in table 3.2. The standard deviation of a single generation 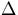 K
is given by,
K
is given by,
| 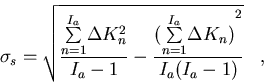 |
(71) |
where Ia is the active number of fission generations up to and including
the current generation. The standard
deviation of the mean is,
| 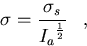 |
(72) |
and is provided with the numerical Monte Carlo results in table 3.2.
Table:
Perturbation Results Using Source Iteration and Correlated Sampling.
| 1|cUnperturbed |
1ccross sections: |
1c |
1c| |
1|c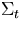 =1.0 cm-1, =1.0 cm-1, |
1c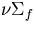 =0.11 cm-1, =0.11 cm-1, |
1c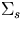 =0.9 cm-1 =0.9 cm-1 |
1c| |
| 1|cProblem # |
1|c|Perturbed cross sections |
1|c|TWODANT 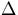 K K |
1c|Monte Carlo 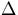 K K |
| 1 |
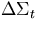 =.001, =.001, 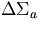 =.001 =.001 |
-.008807 |
-.007401
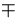 .12E-4 .12E-4 |
| |
|
|
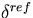 =.0005 =.0005 |
| 2 |
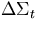 =.0001, =.0001, 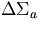 =.0001 =.0001 |
-.000888 |
-.0007462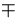 .12E-5 .12E-5 |
| |
|
|
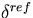 =.0001 =.0001 |
| 3 |
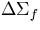 =.0001 =.0001 |
.000903 |
.00082298 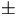 .78E-6 .78E-6 |
| |
|
|
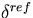 =0. =0. |
Similar to the table 3.1 results, the Monte Carlo runs for table 3.2
are for 30 inactive
batches, 70 active batches, and 2000 neutrons per batch.
We observe from table 3.2 that for the problems analyzed, the
source iteration
method has difficulty estimating the differential effect in eigenvalue. As
mentioned before in section 3.2.1, the problems of table 3.2
will be
solved (in section 3.3.4) using the CSFM method
and will provide significantly improved results.



Next: Correlated Sampling Fission Matrix
Up: Correlated Sampling Technique
Previous: Variance Reduction Using -scatter
Amitava Majumdar
9/20/1999
![]() -scatter cross section is added to the total cross section for each
of the reference,
unperturbed, and perturbed systems to avoid fluctuations in the adjusting
weight
factors. For illustration, the value of
-scatter cross section is added to the total cross section for each
of the reference,
unperturbed, and perturbed systems to avoid fluctuations in the adjusting
weight
factors. For illustration, the value of ![]() is given
along with the perturbation results
in table 3.2. The standard deviation of a single generation
is given
along with the perturbation results
in table 3.2. The standard deviation of a single generation ![]() K
is given by,
K
is given by,