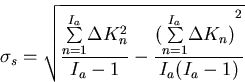Next: Multigroup Energy Transfer
Up: Correlated Sampling Technique
Previous: Correlated Sampling and Source
We have shown in previous sections of this chapter that either (i)
subtracting two independent Monte Carlo simulations or (ii) combining source
iteration and correlated sampling fails to estimate small
perturbation effects with reasonable accuracy. Several references
[Rie88, Sei91, Gal95] point out that
for the calculation of Monte Carlo perturbation effects it is necessary to
utilize the fission matrix method to perform the eigenvalue calculation.
To that end, two fission matrix equations,
and
for the unperturbed and perturbed systems respectively are needed to formulate
and solve for the eigenvalue perturbations:
| 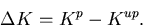 |
(75) |
In the above equations, K is the eigenvalue, S is the fission source vector, and
A is the fission matrix. One approach [Sei91, Gal95] utilizes the linearity of
the transport equation and splits the fission matrix into two parts:
The fission matrix A0 is formed by the particles that do not go through a
perturbed cell during a random walk simulation, whereas the fission matrix A1 is
formed by the particles that arrive from any perturbed cell. Since the
perturbation is confined to the perturbed cells, the matrix A0 is equal in
both the unperturbed and perturbed problems. The matrix A1 is evaluated only
for the
perturbed problem. During particle tracking in the unperturbed system, all
necessary information for particles that enter any perturbed cell are saved.
At the end of the simulation in the unperturbed system, this information is
then used to calculate to the matrix A1 for the perturbed system.
We have taken a different approach in which the correlated sampling technique
is applied to the fission matrix method [Rie88]. The actual Monte Carlo
simulation is done
in an artificial reference system with cross sections that are linear
combination of the
unperturbed and perturbed systems. The  -scatter cross sections
in the forward direction
are used for the reference, unperturbed, and perturbed systems as explained in
section 3.3.1 of this chapter.
For the determination of the fission matrix of the reference system, the
first generation is started with an assumed source distribution and Wref =
1, where Wref is the weight of a reference system particle. Likewise,
the initial weights of the unperturbed (Wup) and
perturbed (Wp) particles are also set to unity. Particle
tracking is carried out only in the reference system and the weights
of the unperturbed and perturbed systems are modified by multiplying them
with appropriate adjusting weight factors, WFup and WFp, respectively,
during the simulation. At
the end of the first generation, source normalization is done for the reference
system particles to stabilize the neutron population. The source
normalization
has no direct effect on other systems, except that the next generation
particles in the
unperturbed and perturbed systems start out with the same weights as
that of
the reference system particles. For the second generation,
the fission neutron production distribution obtained from the
first generation is used for the reference system particles.
The particles in the unperturbed and perturbed systems
also use the same source distribution as that of the reference
system for
the second generation. This process is continued for specified number of
generations. A few of the initial generations are discarded to avoid
bias due to the initial source guess.
-scatter cross sections
in the forward direction
are used for the reference, unperturbed, and perturbed systems as explained in
section 3.3.1 of this chapter.
For the determination of the fission matrix of the reference system, the
first generation is started with an assumed source distribution and Wref =
1, where Wref is the weight of a reference system particle. Likewise,
the initial weights of the unperturbed (Wup) and
perturbed (Wp) particles are also set to unity. Particle
tracking is carried out only in the reference system and the weights
of the unperturbed and perturbed systems are modified by multiplying them
with appropriate adjusting weight factors, WFup and WFp, respectively,
during the simulation. At
the end of the first generation, source normalization is done for the reference
system particles to stabilize the neutron population. The source
normalization
has no direct effect on other systems, except that the next generation
particles in the
unperturbed and perturbed systems start out with the same weights as
that of
the reference system particles. For the second generation,
the fission neutron production distribution obtained from the
first generation is used for the reference system particles.
The particles in the unperturbed and perturbed systems
also use the same source distribution as that of the reference
system for
the second generation. This process is continued for specified number of
generations. A few of the initial generations are discarded to avoid
bias due to the initial source guess.
Now the fission rate is determined. Recall from our discussion on
the fission matrix
algorithm of
chapter 2 that the fission rate is determined by the probability that
a particle starting in volume element l generates al,m particles in
element m, where al,m is an element of the fission matrix A. For
the reference system, the matrix element al,mref is scored as,
| ![\begin{displaymath}
{a_{l,m}^{ref}}={a_{l,m}^{ref}} +
W^{ref}{[{\nu^{ref}\Sigma_f^{ref}}]
\over{[\Sigma_t^{ref} + \delta^{ref}]}}\;\;\;,
\end{displaymath}](img159.gif) |
(77) |
where 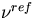 is the number of particles emerging from a fission reaction
in the reference system and
is the number of particles emerging from a fission reaction
in the reference system and 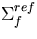 is the macroscopic fission
cross-section for the reference system. At the same time, the fission matrix
elements for the unperturbed and perturbed fission matrices, Aup and
Ap, are estimated as,
is the macroscopic fission
cross-section for the reference system. At the same time, the fission matrix
elements for the unperturbed and perturbed fission matrices, Aup and
Ap, are estimated as,
| ![\begin{displaymath}
{a_{l,m}^{up}}={a_{l,m}^{up}} +
W^{up}{[{\nu^{up}\Sigma_f^{up}}]
\over{[\Sigma_t^{ref} + \delta^{ref}]}}\;\;\;,
\end{displaymath}](img162.gif) |
(78) |
and
| ![\begin{displaymath}
{a_{l,m}^{p}}={a_{l,m}^{p}} +
W^{p}{[{\nu^{p}\Sigma_f^{p}}]
\over{[\Sigma_t^{ref} + \delta^{ref}]}}\;\;\;.
\end{displaymath}](img163.gif) |
(79) |
The dominant eigenvalues Kref, Kup, and
Kp of matrices Aref, Aup and Ap, respectively, are
determined numerically, after which 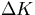 can be calculated as,
can be calculated as,
| 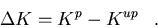 |
(80) |
As before, the standard deviation of the single generation 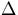 K
is given by,
K
is given by,
| 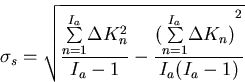 |
(81) |
and the standard deviation of the mean is given by
| 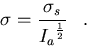 |
(82) |
This  is provided with the numerical Monte Carlo results. Variance
reduction
schemes are applied as explained in section 3.3.2 of this chapter.
is provided with the numerical Monte Carlo results. Variance
reduction
schemes are applied as explained in section 3.3.2 of this chapter.
The perturbation problems of table 3.1 and 3.2 are now solved with the
combined
CSFM technique as described above. These
results are shown in table 3.3. Similar to table 3.1 and 3.2,
the Monte
Carlo runs for table 3.3 utilize 30 inactive
batches, 70 active batches and 2000 neutrons per batch.
Table:
Perturbation Results Using Fission Matrix and Correlated Sampling.
| 1|cUnperturbed |
1ccross sections: |
1c |
1c| |
1|c =1.0 cm-1, =1.0 cm-1, |
1c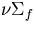 =0.11 cm-1, =0.11 cm-1, |
1c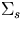 =0.9 cm-1 =0.9 cm-1 |
1c| |
| 1|cProblem # |
1|c|Perturbed cross sections |
1|c|TWODANT  K K |
1c|Monte Carlo  K K |
| 1 |
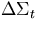 =.001, =.001, 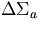 =.001 =.001 |
-.008807 |
-.0089069
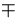 .82E-5 .82E-5 |
| |
|
|
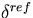 =.0005 =.0005 |
| 2 |
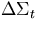 =.0001, =.0001, 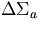 =.0001 =.0001 |
-.000888 |
-.00089601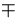 .89E-6 .89E-6 |
| |
|
|
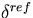 =.0001 =.0001 |
| 3 |
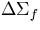 =.0001 =.0001 |
.000903 |
.00090325 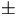 .51E-6 .51E-6 |
| |
|
|
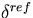 =0. =0. |
Comparing the results of table 3.1 and table 3.2 with that of table 3.3
we observe
that the CSFM technique
provides significantly improved results compared with direct
subtraction or the source iteration method with correlated sampling.



Next: Multigroup Energy Transfer
Up: Correlated Sampling Technique
Previous: Correlated Sampling and Source
Amitava Majumdar
9/20/1999
![]() -scatter cross sections
in the forward direction
are used for the reference, unperturbed, and perturbed systems as explained in
section 3.3.1 of this chapter.
For the determination of the fission matrix of the reference system, the
first generation is started with an assumed source distribution and Wref =
1, where Wref is the weight of a reference system particle. Likewise,
the initial weights of the unperturbed (Wup) and
perturbed (Wp) particles are also set to unity. Particle
tracking is carried out only in the reference system and the weights
of the unperturbed and perturbed systems are modified by multiplying them
with appropriate adjusting weight factors, WFup and WFp, respectively,
during the simulation. At
the end of the first generation, source normalization is done for the reference
system particles to stabilize the neutron population. The source
normalization
has no direct effect on other systems, except that the next generation
particles in the
unperturbed and perturbed systems start out with the same weights as
that of
the reference system particles. For the second generation,
the fission neutron production distribution obtained from the
first generation is used for the reference system particles.
The particles in the unperturbed and perturbed systems
also use the same source distribution as that of the reference
system for
the second generation. This process is continued for specified number of
generations. A few of the initial generations are discarded to avoid
bias due to the initial source guess.
-scatter cross sections
in the forward direction
are used for the reference, unperturbed, and perturbed systems as explained in
section 3.3.1 of this chapter.
For the determination of the fission matrix of the reference system, the
first generation is started with an assumed source distribution and Wref =
1, where Wref is the weight of a reference system particle. Likewise,
the initial weights of the unperturbed (Wup) and
perturbed (Wp) particles are also set to unity. Particle
tracking is carried out only in the reference system and the weights
of the unperturbed and perturbed systems are modified by multiplying them
with appropriate adjusting weight factors, WFup and WFp, respectively,
during the simulation. At
the end of the first generation, source normalization is done for the reference
system particles to stabilize the neutron population. The source
normalization
has no direct effect on other systems, except that the next generation
particles in the
unperturbed and perturbed systems start out with the same weights as
that of
the reference system particles. For the second generation,
the fission neutron production distribution obtained from the
first generation is used for the reference system particles.
The particles in the unperturbed and perturbed systems
also use the same source distribution as that of the reference
system for
the second generation. This process is continued for specified number of
generations. A few of the initial generations are discarded to avoid
bias due to the initial source guess.
![\begin{displaymath}
{a_{l,m}^{ref}}={a_{l,m}^{ref}} +
W^{ref}{[{\nu^{ref}\Sigma_f^{ref}}]
\over{[\Sigma_t^{ref} + \delta^{ref}]}}\;\;\;,
\end{displaymath}](img159.gif)
![\begin{displaymath}
{a_{l,m}^{up}}={a_{l,m}^{up}} +
W^{up}{[{\nu^{up}\Sigma_f^{up}}]
\over{[\Sigma_t^{ref} + \delta^{ref}]}}\;\;\;,
\end{displaymath}](img162.gif)
![\begin{displaymath}
{a_{l,m}^{p}}={a_{l,m}^{p}} +
W^{p}{[{\nu^{p}\Sigma_f^{p}}]
\over{[\Sigma_t^{ref} + \delta^{ref}]}}\;\;\;.
\end{displaymath}](img163.gif)