 magine hearing a rattlesnake but not knowing which direction to run. Proper localization is an essential part of hearing perception, and losing that ability is an unsettling aspect of hearing impairment. Hearing aids can amplify sounds, but they can’t provide the perceptual cues required to ascertain their origin. As part of an effort to restore this sensibility to people who wear hearing devices, NPACI researchers in the Engineering thrust are using mathematically intensive techniques to trace the path acoustic waves take around and through the head. The path subtly alters sounds in a way that allows people with normal hearing to locate the source of sounds. The findings could be used to build customized hearing devices that would enable wearers to locate the sources of sounds.
 |
|
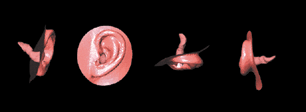
Sound Channel
These are views of the ear canal, as connected to an ear mesh. Produced early in a project to model acoustic pressure around the human head by Leszek Demkowicz and his colleagues, the simulation uses parallel hp-boundary element method generate an image of the middle ear.
|
"Hearing aids are there to improve hearing, but they don’t attempt to address the localization problem," said Chandrajit Bajaj a professor of computer science at the University of Texas, Austin. Bajaj also is the chair in visualization at the Texas Institute of Computational and Applied Mathematics (TICAM), an NPACI partner. Currently, designing and tuning a hearing device that provides localization requires incorporating clues related to location and frequency, a process that involves a trial-and-error approach that depends on the feedback of the wearer. However, for many people, particularly young children, properly tuning a hearing device is virtually impossible.
 |
|
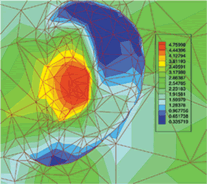
Inner Ear Simulation
The geometrical complexities associated with the ear canal, along with the possibility of singular solutions in such domains, necessitate the use of adaptive finite elements. This simulation shows the pressure distribution within the ear canal in resonance mode, 2900 Hz. Sounds of this frequency create different levels of pressure along the canal, which are represented by the blue-to-red color gradient.
|
Bajaj and Leszek Demkowicz, a fellow researcher at TICAM, have been working on models that determine the pressure on the eardrum depending on the location and frequency of the sound waves. Their work may someday be used to determine how hearing aid design will be based on the size, shape, and other characteristics of an individual’s head.
The human head is shaped irregularly with bone, muscle, and fat–materials that are challenging for researchers to model in order to understand the pattern of acoustic waves passing around it. Modeling requires a twofold approach–carefully mapping the geometry of the head’s surface and describing its interaction with acoustic waves. The computational approach involves draping the head with a digital mesh consisting of fixed points, aiming acoustic waves at those points, and recording the flow.
"We looked at MRI (magnetic resonance imaging) data and used that to reconstruct a model of the human head," said Bajaj. "We did the meshing based on that to show that we could do this in a customized setting. So if one wanted a patient-specific calculation, you could do that."
Bajaj and his colleagues initially worked on mesh geometry, while Demkowicz and his group focused on solving the propagation of waves through it. "To solve the problem accurately, we tweak the modeling of the human head to come up with smooth geometries, and balance that with faster solution techniques so the numerical integration does not suffer," said Bajaj.
MODELING MESH
 |
 |
|
Impact Zones
Most sounds are made up of a complicated mixture of vibrations. A sound spectrum is a representation of a sound–usually a short sample of a sound–in terms of the amount of vibration at each individual frequency. It is usually presented as a graph of either power or pressure as a function of frequency. As the frequency increases, the areas of highest pressure become more and more localized on the impact zone. The warmer colors indicate areas of higher pressure, with red being the most intense, while the cooler colors show the area of lower pressure, with green being the lightest. At higher frequencies (right) the pressure becomes greatest at the ear’s opening, or concha.
|
Bajaj uses a toolbox of geometric modeling and visualization methods to solve the problems. His mesh-generating tools start with a set of two-dimensional images, such as MRI slices, and extract 3-D geometries from them. The object’s geometry is expressed as a mesh, a lattice of tetrahedra or hexahedra (blocks) called finite elements. Such imaging data can be dense, and the goal is to extract the geometry adaptively, providing high resolution only where necessary. The challenge is to do it rapidly for large data sets.
Simulation results must be plotted onto such underlying finite-element meshes. Accelerated isocontouring tools analyze the physical features in the results–such as flow, temperature, stress, or electromagnetic fields–and plot isocontours of functions on the surface mesh. Points on the mesh with the same value are given the same color and transparency, similar to elevation contours on a topographical map. The basic visualization technique is used often by scientists for two-dimensional and 3-D simulation data.
"There are difficulties in modeling the human head, which is the problem of building conforming and smooth meshes from imaging data," said Bajaj. "There also are difficulties in modeling and accurately computing the integration for acoustics scattering."
Currently, Bajaj uses a 128-processor Compaq cluster and a 24-processor Silicon Graphics Onyx 2 at TICAM to perform his simulations. Bigger machines wouldn’t alter the outcomes, but they would more quickly generate the models, which would be important in a clinical setting when a patient is waiting to have a hearing aid customized.
The project was proposed by Rich Charles, then at SDSC, after Demkowicz investigated a variety of acoustic and electromagnetic scattering problems. Demkowicz’s graduate student, Tim Walsh, then picked up the project for his doctoral thesis. For several years, Bajaj’s group, which included visiting scientist Guoliang Xu, worked on the geometric modeling of the head, while Walsh and Demkowicz worked on the solver. Charles provided additional assistance in constructing a geometrical model for the ear channel.
 |
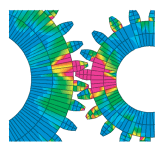From Ears to Gears
The same code used to model the human auditory system, hp-adaptive technology, can be applied to planetary gears. Dynamical behavior of planetary gear train, consisting of a sun gear, four planets, and a carrier, is shown modeled as general dynamic contact/
impact of elastic, nearly rigid bodies. The problem reduces to a successive solution of a large number of single steps. Each single step involves a solution of a large system of linear equations and inequalities. The developed parallel simulator is based on 2Dhp90—the two-dimensional hp code—and has been developed for the Cray 3TE.The work constituted the Ph.D. dissertation of Andrzej Bajer in Demkowicz’s lab. |
After Walsh graduated, Bajaj’s group took over the solution portion of the problem. "In some sense, all the balls are in our court now, which includes all the modeling, meshing, and the solution of the Helmholtz equation," said Bajaj. The Helmholtz equation, one of SDSC’s "grand challenge" equations, is used in acoustics and electromagnetic studies. It arises, for example, in the analysis of vibrating membranes, such as the head of a drum. "We’ve taken Leszek’s work, and we’re pushing it further. We are developing parallel cascadic solvers based on surface and 3-D recursive subdivision schemes. We don’t have the most efficient solver yet, but we are getting there."
Bajaj’s group is fine-tuning its code for the solution, and coupling it to the meshing and visualization codes. The efficiency of the code depends on domain modeling and the fast convergent technique used to compute the numerical solution.
The problem of modeling the human head began in Demkowicz’s lab as part of a larger project working out better ways of solving acoustic and electromagnetic scattering problems. For two decades, J. Tinsley Oden, director of TICAM and leader of the NPACI Engineering thrust, and Demkowicz, a professor in the Department of Aerospace Engineering and Engineering Mechanics at Texas, pioneered the use of adaptive methods that automate the mesh construction process to deliver superb accuracy at low cost.
Working with meshes generally involves changing either the mesh size or the order of approximation. The mesh size is usually referred to by the variable h, and the order of approximation with the variable p, so these methods are usually called h-adaptive and p-adaptive. However, certain common types of engineering problems, such as modeling acoustic and electromagnetic waves, require methods that automatically vary both the size and order of approximation–called hp-adaptive methods.
Demkowicz’s work grew out of earlier research by renowned TICAM mathematician Ivo Babuska, who demonstrated theoretically that an hp-adaptive approach could deliver exponential convergence rates for both regular and irregular solutions. "For the last 13 years, I have been one of rather few people who have tried to translate that theoretical result into a practical engineering tool," said Demkowicz. "Coding hp-methods is extremely challenging."
FROM THEORY TO SOFTWARE
 |
 |
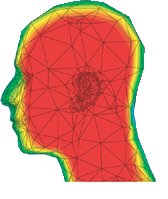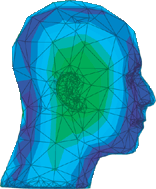
Acoustic Pressure Profiles
NPACI researchers have been applying hp-adaptive boundary element methods to the acoustics of the human auditory system. The goal of the project is to determine the acoustic pressure on the eardrum. The so-called acoustic transfer functions are used to design and tune hearing devices. The tuning is especially challenging in children for whom the “trial and error” approach is virtually impossible.
LEFT: This head shows the pressure distribution in the “shadow” zone resulting from a plane wave at 500 Hz, at normal incidence.
RIGHT: This image shows the pressure distribution in the “impact” zone at the same frequency. The peak in pressure around the ear is referred to as the “bright spot.” |
To illustrate the difficulty of the problem, Demkowicz tells the story of a 150-page paper written by German mathematician Leo Korn on a fundamental mathematical result now known as Korn’s inequality. Hermann Weyl, a leading mathematician at the time, said he was able to read only the first 50 pages of the article. "That paper provided a foundation for the entire modern theory of elasticity," said Demkowicz. He notes that functional analysis and partial differential equations, which were developed later, now allow the same theory to be proven in less than two pages.
Oden, Demkowicz, and their colleagues have incorporated advanced mathematics into versions of the two-dimensional and 3-D hp finite-element code for the first time. The codes eventually resulted in PHLEX, the first hp-adaptive finite-element commercial software, developed at the Computational Mechanics Company. Applications included a variety of complex problems in solid and fluid mechanics, focusing especially on supersonic compressible flows.
For the past four years, they have been working on parallel implementation on memory-distributed platforms, such as the Cray T3E, which has included an evolution through three programming languages and versions of the code. "The idea has been to minimize changes in the data structure and to recycle as much as possible of our existing software," said Demkowicz. "It is a painful learning process."
Part of that pain was trying to build on a successful code for modeling two-dimensional objects. Inspired at an NPACI All-Hands Meeting, Demkowicz developed a new 3-D data structure. "After that came the breakthrough with automatic adaptivity," he said. The code became "smart" enough to control the error and modify the discretization accordingly. Rather than just using the h-refinements (breaking elements) or the p-refinements (increasing locally polynomial degree), he could use both. His simulations begin with a coarse mesh, solve the problem, estimate the error, and then generate an adaptively refined mesh. The process is repeated until the error declines to an acceptable level. "With hp-methods, the choice is much more subtle," he said. "You have to choose not only where to refine, but also how to refine. Many people working on the subject say this is impossible to accomplish."
Four hp finite-element codes (2Dhp90, 2Dhp90_EM, 3Dhp90, and 3Dhp90_EM) have been developed, documented, and placed on the Web. The Swiss Federal Institute of Technology in Zurich, the Aeronautical Research Institute of Sweden in Schlumberger, the University of Cracow, the U.S. Navy, and other institutions use them for teaching and research. The codes also have provided a basis for specific applications cofunded within NPACI: modeling acoustics and the human auditory system, modeling of planetary gears, and 3-D electromagnetic simulations using FE, and coupled FE/IE methods.
THE NEXT STEP
Bajaj wants to model the entire human auditory system. Once the framework for understanding the interaction of acoustic pressure on the eardrum is complete, the next step will be to continue farther along the ear canal. "It’s like you have this entire musical system," he said. "Everything along the pipeline has to be modeled if you want to come up with a comprehensive model of the human auditory system. Clearly, modeling the acoustic pressure on the eardrum is just one step. The next thing is to model the dynamic of how the sounds get amplified within the tunnel and finally how it gets beautifully spread out into a spectrum in the cochlea."
"It’s little epsilons that we are doing," said Bajaj. "As our ability to use computers to prototype various physical phenomena improves, including acoustic scattering, we can make those solutions very numerically robust and customize them for individual patients."–CF 
|
PROJECT LEADERS
Leszek Demkowicz, Chandrajit Bajaj
University of Texas, Austin
PARTICIPANTS
Adam Zdunek
Aeronautical Institute of Sweden
Richard Charles
SDSC
James Demmel
UC Berkeley
Waldek Rachowicz
Cracow University of Technology, Poland
Peter Monk
University of Delaware
Ulrich Langer,
Joachim Schoeberl
University of Linz, Austria
John Volakis,
Edward Davidson
University of Michigan
Daniele Boffi
University of Pavia, Italy
Ivo Babuska,
Andrzej Bajer,
Satish Chavva,
Hao Ling,
Dean Neikirk,
Waldek Rachowicz,
Jessica Sun,
Timothy Walsh, Guoliang Xu
University of Texas, Austin
Jack Lancaster
University of Texas Medical Center,
San Antonio
|
Skip to navigation
